![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
多次元フーリエ変換 のバックアップ(No.5) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
多次元フーリエ変換 のバックアップ(No.5) |
多次元フーリエ変換 |
正変換: |
|
例えば、正変換に関して、全領域におけるスカラ場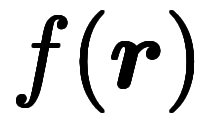
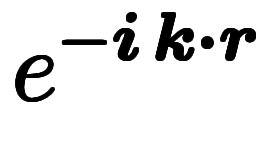 の線積分が存在するならば、
の線積分が存在するならば、
積分領域の表記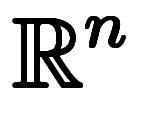 と
と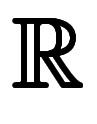 で区別しかない。
で区別しかない。
全領域の意味で

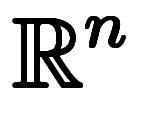 の表記を使うと全くの同形になってしまう。
の表記を使うと全くの同形になってしまう。
|
|
体積分の表記には微小体積 の専用記号を設ける手法が一般的ではあるが、
の専用記号を設ける手法が一般的ではあるが、
基底の情報を含まないため、空間領域と角波数領域の区別が求められるフーリエ変換では役不足。
そのため、基底の情報を持った位置ベクトル や
や *2を使われているものの、
*2を使われているものの、
今度は位置ベクトルは線積分の表記でも用いられるために記号衝突が起きる*3。
これに対し、凌宮数学では外積代数に基づく基底積の表記法があり、
基底積を使えば、空間領域と角波数領域を書き分けながら、線積分・体積分も書き分けられる。
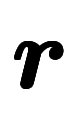 が空間領域における位置ベクトルであるように、
が空間領域における位置ベクトルであるように、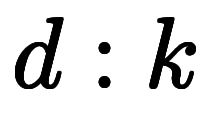 は波数領域における位置ベクトルである。
は波数領域における位置ベクトルである。


位置ベクトル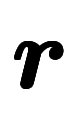 に対し、微小変位ベクトル
に対し、微小変位ベクトル が定義でき、
が定義でき、
各次元におけるウェッジ積により最高次数のウェッジ積は以下のようになる。
1次元 |
|
|
2次元 |
|
|
3次元 |
|
|
4次元 |
|
|
同様に角波数ベクトル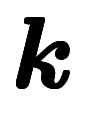 に対し、微小角波数ベクトル
に対し、微小角波数ベクトル が定義でき、
が定義でき、
各次元におけるウェッジ積により最高次数のウェッジ積は以下のようになる。
1次元 |
|
|
2次元 |
|
|
3次元 |
|
|
4次元 |
|
|
基底積の表記には、空間を表す基底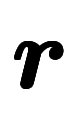 と
と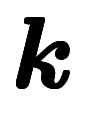 を含むため、空間を書き分けできる。
を含むため、空間を書き分けできる。
また、微小の次数を含むため、線積分とも書き分けできる。
この表記を多次元フーリエ変換の式に適応すると、以下のようになる:
正変換: |
|
特に、4次元時空間領域に関しては次の分離表記にも柔軟に対応できる。
正変換: |
|