![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
基底積 |
基底積 |
1次形式 |
これは、微小ベクトルの外積の成分側は というであると理解できる。また、
というであると理解できる。また、 は個々の形式において通常ベクトルの演算のどれかに対応している。非常に単純な関係だが、2種類の外積を区別しない限り簡単に見えてこない。
は個々の形式において通常ベクトルの演算のどれかに対応している。非常に単純な関係だが、2種類の外積を区別しない限り簡単に見えてこない。
しかし、例えば![[ d\:S | \:A \wxv \:B ] $$ [ d\:S | \:A \wxv \:B ] $$](./eq/eq-ni-bd683d468a4152dc155f8d1e06a84f0a.png) という表現は成分側は等号の左側の成分側を演算子で結んでいる形をしているのに、基底側は等号の左側に無い記号を使っていて、バランスが悪い。そこで、基底側にも成分側と同様に
という表現は成分側は等号の左側の成分側を演算子で結んでいる形をしているのに、基底側は等号の左側に無い記号を使っていて、バランスが悪い。そこで、基底側にも成分側と同様に 演算子を形式的に定義してあげると、以下のように微小ベクトルの外積
演算子を形式的に定義してあげると、以下のように微小ベクトルの外積 が
が と
と に分割され、それぞれの計算法則に従って計算されるように見える。ここで、
に分割され、それぞれの計算法則に従って計算されるように見える。ここで、 は基底側の積のため、基底積と呼ぶ。
は基底側の積のため、基底積と呼ぶ。
1次形式 |
記号の由来は の基底側に現われる積のために似せているが、
の基底側に現われる積のために似せているが、 は
は と同じく外積空間を作る外積ではあるのに対し、
と同じく外積空間を作る外積ではあるのに対し、 は計算法則が異なる。今は基底積の演算法則は重要ではないが、一応3次元の場合は成分表示をすると次のようになる。微小ベクトルの外積として計算し、その微小基底と対応する通常基底を並べただけである。
は計算法則が異なる。今は基底積の演算法則は重要ではないが、一応3次元の場合は成分表示をすると次のようになる。微小ベクトルの外積として計算し、その微小基底と対応する通常基底を並べただけである。
微小ベクトルの1次形式 |
微小ベクトルの1次形式 |
微小ベクトルの1次形式 |



基底積を用いれば、以下のように、全ての微小基底を のみの基底積で表せる。
のみの基底積で表せる。
|
|
|
積がこの形になれば、累乗で書きたくなるのが数学的センスである。しかし、 は既にベクトルの内積
は既にベクトルの内積 を意味する表記として頻繁に用いられるため、
を意味する表記として頻繁に用いられるため、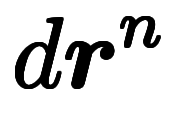 の形で書くのは避けたい。そこで、猫式では、基底積の累乗を
の形で書くのは避けたい。そこで、猫式では、基底積の累乗を 、または略して
、または略して と表記する*1。また、便宜上、
と表記する*1。また、便宜上、

 と決める。
と決める。
これより、基底積の演算は次のようになり、
1次形式 |
1次形式 
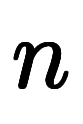 次形式の統一表現を得る。
次形式の統一表現を得る。
|
さらに、ストークスの定理とガウスの定理は次のように表記できる。
|
|
|
|
|
|
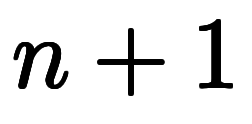 階から
階から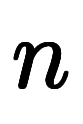 階に下る置換積分の統一表現は次のようになる。ただし、
階に下る置換積分の統一表現は次のようになる。ただし、 は
は 次元の超空間、
次元の超空間、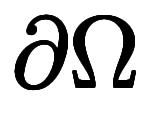 はそれを囲む
はそれを囲む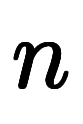 次元超空間。
次元超空間。
|
|
|
この表記であれば、微分 の
の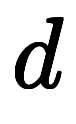 が
が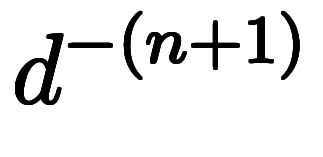 と打ち消し、
と打ち消し、 が
が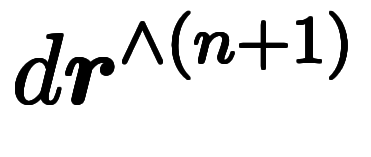 と打ち消す感覚で等式の左辺から右辺を組み立てられる。
と打ち消す感覚で等式の左辺から右辺を組み立てられる。



前々回、ベクトル置換積分では無理やりに

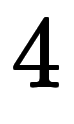 のような計算を通した。前回、基底成分表記では合法な手法で
のような計算を通した。前回、基底成分表記では合法な手法で

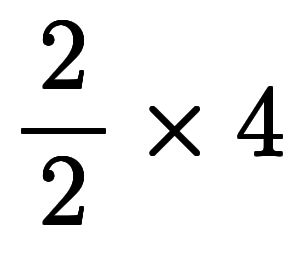

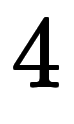 のような計算をした。そして今回、表記自体を見直し、同じ式を
のような計算をした。そして今回、表記自体を見直し、同じ式を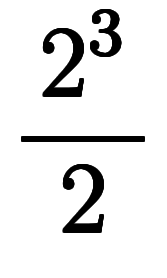

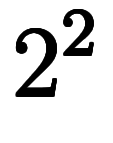 のように変えた。その結果、全ての微小要素が
のように変えた。その結果、全ての微小要素が の形で記述され、置換積分はその指数(階数)を
の形で記述され、置換積分はその指数(階数)を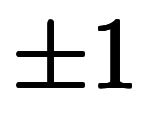 する公式になった。
する公式になった。
ところが、3次元空間では基底積の演算は3通りあるのに置換積分の公式は2つしかなく、1次形式 0次形式の式に対応した置換積分がまだ登場してない。次回は
0次形式の式に対応した置換積分がまだ登場してない。次回は に対応する積分と、
に対応する積分と、 と
と を結ぶ置換積分公式について考える。
を結ぶ置換積分公式について考える。