![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
点積分 |
点積分ベクトル解析で線積分、面積分、体積分とあるのに、点積分ないのが不思議。線、面、体で、1次元、2次元、3次元なら、点は0次元に対応しているはず。0は無を意味するが、扱わなければ今の数学は無い。 猫式では、以下の類推で、点積分なる積分を形式的に定義する。
点積分では、積分の回数を表す 積分の基本定理と |
| 基底積表記 | 慣用名 | 通常表記 | |
|---|---|---|---|
| 点線 置換 | ![\inte[P] $$ \inte[P] $$](./eq/eq-ni-2ab83b26f02d30bea1a1a8b5fdac4b8a.png) 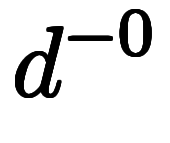     ![\inte[R] $$ \inte[R] $$](./eq/eq-ni-36407cd8870cb013ab519e692d6f8e33.png) 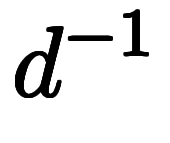    | 積分の基本定理 | 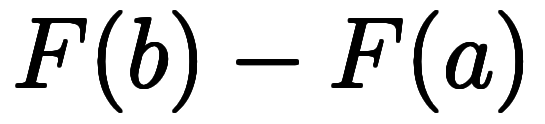  ![\inte[a]^b $$ \inte[a]^b $$](./eq/eq-ni-6acd562f3f50bde871ab6469e281cb41.png)    |
| 線面 置換 | ![\inte[R] $$ \inte[R] $$](./eq/eq-ni-36407cd8870cb013ab519e692d6f8e33.png) 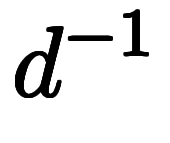     ![\inte[S] $$ \inte[S] $$](./eq/eq-ni-3311dd4ae3ec7a06c74300f9e3899470.png) 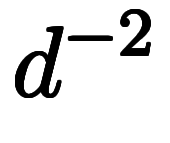    | ストークスの定理 | ![\inte[R] $$ \inte[R] $$](./eq/eq-ni-36407cd8870cb013ab519e692d6f8e33.png)     ![\inte[S] $$ \inte[S] $$](./eq/eq-ni-3311dd4ae3ec7a06c74300f9e3899470.png) 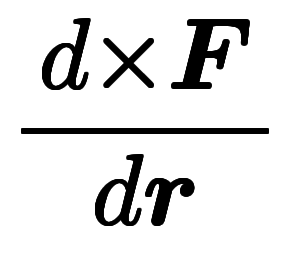   |
| 面体 置換 | ![\inte[S] $$ \inte[S] $$](./eq/eq-ni-3311dd4ae3ec7a06c74300f9e3899470.png) 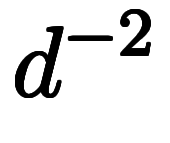     ![\inte[V] $$ \inte[V] $$](./eq/eq-ni-50972de713104e35c790025260ba8251.png) 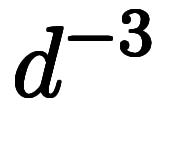    | ガウスの定理 | ![\inte[S] $$ \inte[S] $$](./eq/eq-ni-3311dd4ae3ec7a06c74300f9e3899470.png)     ![\inte[V] $$ \inte[V] $$](./eq/eq-ni-50972de713104e35c790025260ba8251.png)    |
積分の基本定理とは普通1次元で![\inte[a]^b $$ \inte[a]^b $$](./eq/eq-ni-6acd562f3f50bde871ab6469e281cb41.png)
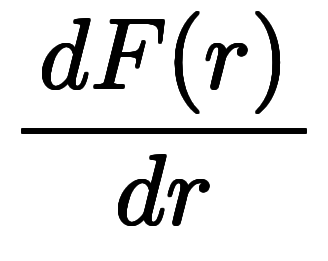


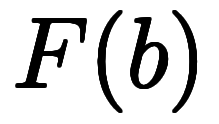

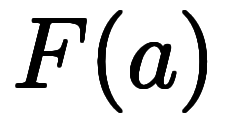 を指す。ベクトル場では
を指す。ベクトル場では![\inte[\:a]^{\:b} $$ \inte[\:a]^{\:b} $$](./eq/eq-ni-01ecba8ca1a1ab42e65afb798ffe8830.png)
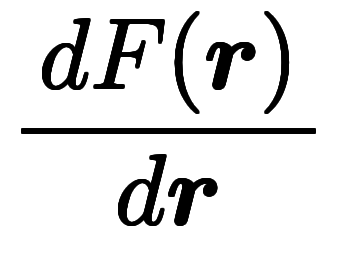



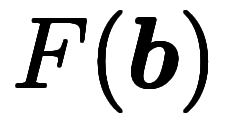

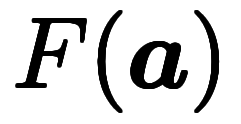 が成り立ち、そのベクトル版にあたる。点積分を使えば、大雑把に
が成り立ち、そのベクトル版にあたる。点積分を使えば、大雑把に![\inte[\:a]^{\:b} $$ \inte[\:a]^{\:b} $$](./eq/eq-ni-01ecba8ca1a1ab42e65afb798ffe8830.png)

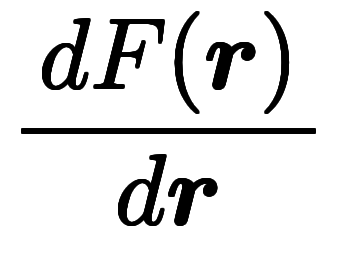


![\inte[\:a]^{\:b} $$ \inte[\:a]^{\:b} $$](./eq/eq-ni-01ecba8ca1a1ab42e65afb798ffe8830.png)
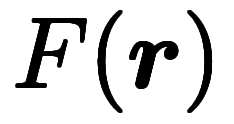 。
。
厳密には、通常の線積分の![\inte[a]^b $$ \inte[a]^b $$](./eq/eq-ni-6acd562f3f50bde871ab6469e281cb41.png) は
は から
から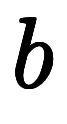 までの区間
までの区間![\inte[R] $$ \inte[R] $$](./eq/eq-ni-36407cd8870cb013ab519e692d6f8e33.png) 、点積分の
、点積分の![\inte[a]^b $$ \inte[a]^b $$](./eq/eq-ni-6acd562f3f50bde871ab6469e281cb41.png) は
は と
と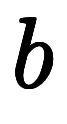 の2点
の2点![\inte[P] $$ \inte[P] $$](./eq/eq-ni-2ab83b26f02d30bea1a1a8b5fdac4b8a.png) と意味が微妙に異なる。猫式では、区別するため、次のように線積分を不定積分と点積分に分けて考え、
と意味が微妙に異なる。猫式では、区別するため、次のように線積分を不定積分と点積分に分けて考え、![\inte[a]^b $$ \inte[a]^b $$](./eq/eq-ni-6acd562f3f50bde871ab6469e281cb41.png) は常に点の範囲指定と読む。
は常に点の範囲指定と読む。
|
| 左側は猫式、右側は対応する通常表記 |
|
| 線積分を不定積分と点積分に分離 |
|
| 不定積分実行 |
|
| 点積分/代入実行 |
この解釈では、![\inte[a]^b $$ \inte[a]^b $$](./eq/eq-ni-6acd562f3f50bde871ab6469e281cb41.png) は定積分の
は定積分の![\left[ \fracstrut \cdots \right]_a^b $$ \left[ \fracstrut \cdots \right]_a^b $$](./eq/eq-ni-25bf90542d26843d7ca3cac4eb3e388d.png) と等価になる。一般に、線積分の被積分関数が
と等価になる。一般に、線積分の被積分関数が と書けない限り*1、積分値は経路に依存し、2つの端点だけでは決まらない。このためにも、1次元という特殊な場合でも
と書けない限り*1、積分値は経路に依存し、2つの端点だけでは決まらない。このためにも、1次元という特殊な場合でも![\inte[a]^b $$ \inte[a]^b $$](./eq/eq-ni-6acd562f3f50bde871ab6469e281cb41.png) は2つの端点の表現であって、区間ではないと考えた方が良い。
は2つの端点の表現であって、区間ではないと考えた方が良い。
以上、基本に戻ったところで、全てのベクトル積分とそれらを結ぶ置換積分公式が出揃う。
3次元空間では次のように纏まる:
| ベクトル積分 | 置換積分公式 | ||
|---|---|---|---|
| 点積分 | ![\inte[P] $$ \inte[P] $$](./eq/eq-ni-2ab83b26f02d30bea1a1a8b5fdac4b8a.png)  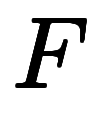   | ||
| 点線置換 | ![\inte[P] $$ \inte[P] $$](./eq/eq-ni-2ab83b26f02d30bea1a1a8b5fdac4b8a.png)  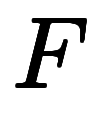    ![\inte[R] $$ \inte[R] $$](./eq/eq-ni-36407cd8870cb013ab519e692d6f8e33.png) 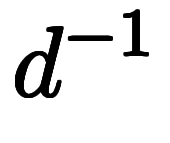    | ||
| 線積分 | ![\inte[R] $$ \inte[R] $$](./eq/eq-ni-36407cd8870cb013ab519e692d6f8e33.png) 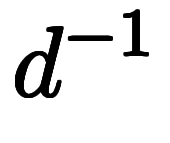    | ||
| 線面置換 | ![\inte[R] $$ \inte[R] $$](./eq/eq-ni-36407cd8870cb013ab519e692d6f8e33.png) 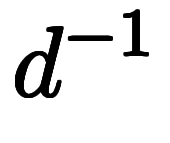     ![\inte[S] $$ \inte[S] $$](./eq/eq-ni-3311dd4ae3ec7a06c74300f9e3899470.png) 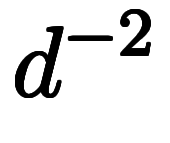    | ||
| 面積分 | ![\inte[S] $$ \inte[S] $$](./eq/eq-ni-3311dd4ae3ec7a06c74300f9e3899470.png) 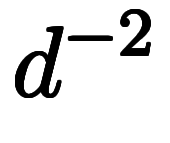    | ||
| 面体置換 | ![\inte[S] $$ \inte[S] $$](./eq/eq-ni-3311dd4ae3ec7a06c74300f9e3899470.png) 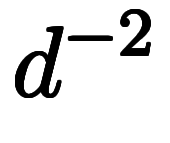     ![\inte[V] $$ \inte[V] $$](./eq/eq-ni-50972de713104e35c790025260ba8251.png) 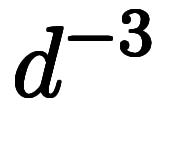    | ||
| 体積分 | ![\inte[V] $$ \inte[V] $$](./eq/eq-ni-50972de713104e35c790025260ba8251.png) 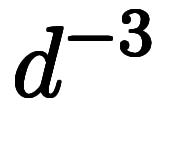 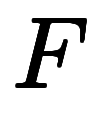   | ||