導入 


3次元空間ではベクトル積分として、線積分![\inte[R] \b F \sx d\:r $$ \inte[R] \b F \sx d\:r $$](./eq/eq-ni-16d1ba8c7709a52bada8a9fd1a66d272.png) 、面積分
、面積分![\inte[S] \b F \sx d\:S $$ \inte[S] \b F \sx d\:S $$](./eq/eq-ni-e680360b4b75900b94a5b36437dc2843.png) 、体積分
、体積分![\inte[V] F \, d V $$ \inte[V] F \, d V $$](./eq/eq-ni-810d8e217290c448b7b93b433cbb44f2.png) がある。
がある。
これらを繋げる公式として、ストークスの定理![\inte[R] \b F \sx d\b r $$ \inte[R] \b F \sx d\b r $$](./eq/eq-ni-5fad66952913cdb79c319e6bc2e1d6d7.png) =
=![\inte[S] \nabla \vx \b F \sx d\b S $$ \inte[S] \nabla \vx \b F \sx d\b S $$](./eq/eq-ni-64ace8ceb1570e0f1535a1d7517e72d1.png) 、ガウスの定理
、ガウスの定理![\inte[S] \b F \sx d\b S $$ \inte[S] \b F \sx d\b S $$](./eq/eq-ni-297029a07ea1238a9ca1eee66f79d173.png) =
=![\inte[V] \nabla \sx \b F \, d V $$ \inte[V] \nabla \sx \b F \, d V $$](./eq/eq-ni-6f4e537470e94b9400bf5daa3b1b7868.png) がある。これらを覚えるのは結構大変で、複雑な図形か成分計算の説明が一般的で理解するのも苦労が多い。
がある。これらを覚えるのは結構大変で、複雑な図形か成分計算の説明が一般的で理解するのも苦労が多い。
また、これらの置換積分を正しく扱うには、外積代数と微分形式を使う必要がある。しかし、これまた表記の問題で、通常のベクトル計算との橋渡しが上手くいかない。
そこで、猫式では積分から微分形式の表記を改善し、上記の積分と公式を含め、1次元のスカラから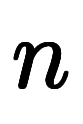 次元のベ積分と置換積分公式を統一的に記述する。さらに、一般的に積分の基本定理と呼ばれる公式を置換積分として纏めて扱う。
次元のベ積分と置換積分公式を統一的に記述する。さらに、一般的に積分の基本定理と呼ばれる公式を置換積分として纏めて扱う。
目次 


![[PukiWiki] [PukiWiki]](image/NekoPunch.png)