基底成分表記 < ベクトル積分

基底成分表記

ベクトルの成分表記には、列ベクトル $\arrs{F_x \\ F_y \\ F_z}$ 、線形結合 $F_x \:e_x + F_y \:e_y + F_z \:e_z$ 、総和規約 $F_i \:e^i$ があり、普通はこの順番で習う。列ベクトルは基底を省いた表記で、直観的で初心者に易しいため、最初に習う*1。その後、座標変換などを扱うとき、基底を省いた裏目で対応できず、ベクトルの基本表現である線形結合を覚えさせられる。続いて、線形結合は記述量が多くて大変なため、すぐに成分計算の頂点に立つ総和規約を叩き込まれる。しかし、総和規約の計算は添字計算の嵐で、機械的に計算が進むのは良いが、直観的ではなく、基底間の対応と成分間の対応と式の意味が確認しにくい。

これに対し、猫式ではベクトルを $\arrb{ \:e_x & F_x \\ \:e_y & F_y \\ \:e_z & F_z }$ と表記。列ベクトルのように基底と成分の両方を並べ、縦線で分離。基底と成分の位置さえ対応していれば、 $\arrb[cc|cc]{ \:e_x & & F_x \\ \:e_y & \:e_z & F_y & F_z }$ のような不規則な並びも許す*2。

*1 厳密には、高校では成分を横に並べた横ベクトル $$ (F_x, F_y, F_z) $$

が一番最初だが、行列表記としては同類。
*2 これを許すと、テンソル積に基づく内積と外積の計算を直観的に記述できる。

混合基底

一般に、線積分は $\inte[R]$ $\:F$ $\sx$ $\:r$ $$ = $$ $\inte[R]$ $\arrs{ F_x \\ F_y \\ F_z }$ $\sx$ $\arrs{ d x \\ d y \\ d z }$ となるが、基底成分表記では $\inte[R]$ $\arrb{ \:e_x & F_x \\ \:e_y & F_y \\ \:e_z & F_z }$ $\sx$ $\arrb{ \:e_x & d x \\ \:e_y & d y \\ \:e_z & d z }$ になる。

通常、基底と言えば $\:e_x$ 、 $\:e_y$ 、 $\:e_z$ を指すが、微分形式では、 $$ dx $$ 、 $$ dy $$ 、 $$ dz $$ を基底と見なしてベクトル演算を行う。このため、ベクトル積分には２種類の基底が混在していることになる。猫式では、区別のため、通常空間の広がりを表す $\:e_x$ 、 $\:e_y$ 、 $\:e_z$ を通常基底またはマクロ基底と、微小空間の広がりを表す $$ dx $$ 、 $$ dy $$ 、 $$ dz $$ を微小基底またはミクロ基底と呼び分ける。対応して、 $\arrb{ \:e_x & F_x \\ \:e_y & F_y \\ \:e_z & F_z }$ 、 $\arrb{ d x & F_x \\ d y & F_y \\ d z & F_z }$ 、 $\arrb{ \:e_x & d x \\ \:e_y & d y \\ \:e_z & d z }$ のように、通常基底のみ、微小基底のみ、両方の基底を含むベクトルをそれぞれ、通常ベクトル、微小ベクトル、混合ベクトルと呼ぶ。

また、混合ベクトルの一般型として、 $\arrb[c|c|c] { \:e_x & dx & F_x \\ \:e_y & dy & F_y \\ \:e_z & dz & F_z }$ $$ = $$ $\arrb { \:e_x dx & F_x \\ \:e_y dy & F_y \\ \:e_z dz & F_z }$ $$ = $$ $\arrb { \:e_x & dx F_x \\ \:e_y & dy F_y \\ \:e_z & dz F_z }$ $$ = $$ $\arrb { dx & \:e_x F_x \\ dy & \:e_y F_y \\ dz & \:e_z F_z }$ $$ = $$ $\arrs { dx \:e_x F_x \\ dy \:e_y F_y \\ dz \:e_z F_z }$ のように表現する。３つ区切りは基底毎の位取り表記、２つ区切りは基底側に書く基底に対するハイライト表記、区切り無しは基底と成分を気にせずに項を並べただけの表記。

ベクトルの積

混合基底の演算もベクトル同様に、通常ベクトル演算、微小ベクトル演算、混合ベクトル演算と分類できる。実際、ベクトル置換積分で登場するのは３種類の通常ベクトル演算と３種類の微小ベクトル演算のみで、混合ベクトル演算は出番無し。その６種類の演算は以下の通り。

通常ベクトルの倍積 $\arrb{\:e_x & A_x \\ \:e_y & A_y \\ \:e_z & A_z}$ $\arrb{1 & B }$ $\arrb{\:e_x & A_x B \\ \:e_y & A_y B \\ \:e_z & A_z B}$	１次形式 $\wx$ ０次形式 $\arrb{dx & A_x \\ dy & A_y \\ dz & A_z}$ $\wx$ $\arrb{1 & B }$ $\arrb{dx & A_xB \\ dy & A_yB \\ dz & A_zB }$
通常ベクトルの外積 $\arrb{\:e_x & A_x \\ \:e_y & A_y \\ \:e_z & A_z}$ $\vx$ $\arrb{\:e_x & B_x \\ \:e_y & B_y \\ \:e_z & B_z}$ $\arrb{ \:e_x & A_y B_z - A_z B_y \\ \:e_y & A_z B_x - A_x B_z \\ \:e_z & A_x B_y - A_y B_x }$	１次形式 $\wx$ １次形式 $\arrb{dx & A_x \\ dy & A_y \\ dz & A_z}$ $\wx$ $\arrb{dx & B_x \\ dy & B_y \\ dz & B_z}$ $\arrb{ dydz & A_y B_z - A_z B_y \\ dxdy & A_z B_x - A_x B_z \\ dydx & A_x B_y - A_y B_x }$
微小ベクトルの内積 $\arrb{\:e_x & A_x \\ \:e_y & A_y \\ \:e_z & A_z}$ $\Sx$ $\arrb{\:e_x & B_x \\ \:e_y & B_y \\ \:e_z & B_z}$ $\arrb{ \fracstrut\,1\,& A_x B_x + A_y B_y + A_z B_z}$	１次形式 $\wx$ ２次形式 $\arrb{dx & A_x \\ dy & A_y \\ dz & A_z}$ $\wx$ $\arrb{ dydz & B_{yz} \\ dzdx & B_{zx} \\ dxdy & B_{xy} }$ $\arrb{ \fracstrut dxdydz & A_x B_{yz} + A_y B_{zx} + A_z B_{xy}}$

一般的に、通常基底にも $\wx$ を適用できる。むしろ、通常ベクトルの倍積、外積、内積を先に $\wx$ で纏めてから微分形式に応用するのが正統である。しかし、この手順では $\wx$ が通常基底と微分基底の両方に使われるため、混同が起こる。実際、ベクトル解析学の授業では微分形式を使わないし、微分形式の授業では通常ベクトルの計算が常に展開されてる状態にしていて、混合ベクトルを上手く回避している。しかし、これでは科目間に深い溝が出来てしまい、理解の妨げとなる。

そこで、微小基底の $\wx$ と区別するべく、猫式では通常ベクトルに適用する $\wx$ を $\wxv$ と表記する。これより、通常ベクトルに関する外積演算は以下となる。

通常ベクトルの１次形式 $\wxv$ ０次形式（倍積）
$\arrb{\:e_x & A_x \\ \:e_y & A_y \\ \:e_z & A_z}$ $\wxv$ $\arrb{1 & B }$ $$ = $$ $\arrb{\:e_x & A_xB \\ \:e_y & A_yB \\ \:e_z & A_zB }$

通常ベクトルの１次形式 $\wxv$ １次形式（外積）
$\arrb{\:e_x & A_x \\ \:e_y & A_y \\ \:e_z & A_z}$ $\wxv$ $\arrb{\:e_x & B_x \\ \:e_y & B_y \\ \:e_z & B_z}$ $$ = $$ $\arrb{ \:e_y\:e_z & A_y B_z - A_z B_y \\ \:e_x\:e_y & A_z B_x - A_x B_z \\ \:e_y\:e_x & A_x B_y - A_y B_x }$

通常ベクトルの１次形式 $\wxv$ ２次形式（内積）
$\arrb{\:e_x & A_x \\ \:e_y & A_y \\ \:e_z & A_z}$ $\wxv$ $\arrb{ \:e_y\:e_z & B_{yz} \\ \:e_z\:e_x & B_{zx} \\ \:e_x\:e_y & B_{xy} }$ $$ = $$ $\arrb{ \fracstrut \:e_x\:e_y\:e_z & A_x B_{yz} + A_y B_{zx} + A_z B_{xy}}$

２次形式と３次形式の基底が少し変わっているが、こっちの方が厳密的であるだけで、今は余り気にせずに通常ベクトル基底の２種類の表現を等価と思って構わない*3。

*3 この違いを扱うには、双対基底の知識が必要になる。その話は気が向いたらする予定。

成分基底表記によるストークスの定理の計算

ストークスの定理は、猫式の基底成分表記とベクトル積分演算子で表記すると次のようになる。ただ、３次元を扱う限り、倍積、外積、内積の方が敷居が低いため、まだ $\wx$ を使わないでおく。

$\inte[S]$ $d^{-2}$ $\arrb{ \:e_x & \fracstrut \ppd{}{x} \\ \:e_y & \fracstrut \ppd{}{y} \\ \:e_z & \fracstrut \ppd{}{z} }$ $\vx$ $\arrb{ \:e_x & \fracstrut F_x \\ \:e_y & \fracstrut F_y \\ \:e_z & \fracstrut F_z }$ $\sx$ $\arrb{ \:e_x & \fracstrut d y d z \\ \:e_y & \fracstrut d z d x \\ \:e_z & \fracstrut d x d y }$ $$ = $$ $\inte[R]$ $$ d^- $$ $\arrb{ \:e_x & F_x \\ \:e_y & F_y \\ \:e_z & F_z }$ $\sx$ $\arrb{ \:e_x & d x \\ \:e_y & d y \\ \:e_z & d z }$

左辺 $$ = $$

$\inte[S]$ $d^{-2}$ $\arrb{ \:e_x & \ppd{F_z}{y} - \ppd{F_y}{z} \\ \:e_y & \ppd{F_x}{z} - \ppd{F_z}{x} \\ \:e_z & \ppd{F_y}{x} - \ppd{F_x}{y} }$ $\sx$ $\arrb{ \:e_x & dydz \\ \:e_y & dzdx \\ \:e_z & dxdy }$	外積を実行
$\inte[S]$ $d^{-2}$ $\arrb{ 1 & dydz \left( \ppd{F_z}{y} - \ppd{F_y}{z} \right) \\ 1 & dzdx \left( \ppd{F_x}{z} - \ppd{F_z}{x} \right) \\ 1 & dxdy \left( \ppd{F_y}{x} - \ppd{F_x}{y} \right) }$	内積を実行
$\inte[S]$ $d^{-2}$ $\arrb{ dydz & \ppd{F_z}{y} - \ppd{F_y}{z} \\ dzdx & \ppd{F_x}{z} - \ppd{F_z}{x} \\ dxdy & \ppd{F_y}{x} - \ppd{F_x}{y} }$	微小基底にハイライトココから、微小基底の計算を開始微分形式では普通この段階から扱い始める
$\inte[S]$ $d^{-2}$ $\arrb{ dx & \ppd{}{x} \\ dy & \ppd{}{y} \\ dz & \ppd{}{z} }$ $\wx$ $\arrb{ dx & F_x \fracstrut \\ dy & F_y \fracstrut \\ dz & F_z \fracstrut }$	１次形式 $\wx$ １次形式に分解
$\inte[S]$ $d^{-2}$ $\arrb{ dx & F_x \\ dy & F_y \\ dz & F_z }$	外微分演算子の定義、もしくは、全微分の関係、もしくは、連鎖則のセンスより、 $d\:r \sx \ddd{}{\:r}$ は０次形式のため、 $\wx$ は省略可能

$\inte[S]$ $\arrb{ dx & F_x \\ dy & F_y \\ dz & F_z }$	について累次積分を実行積分領域を適当に再解釈微小基底の計算はココまで
$\inte[R]$ $\arrb{ 1 & dx F_x \\ 1 & dy F_y \\ 1 & dz F_z }$ $\inte[R] d^- \arrb{ \:e_x \sx \:e_x & dx F_x \\ \:e_y \sx \:e_y & dy F_y \\ \:e_z \sx \:e_z & dz F_z }$	再び通常基底にハイライト、通常基底を挿入このような割り込みは一般的に成立しないが、各成分に微小基底があるため、ここは可能
$\inte[R]$ $\arrb{ \:e_x & dx \\ \:e_y & dy \\ \:e_z & dz }$ $\sx$ $\arrb{ \:e_x & F_x \\ \:e_y & F_y \\ \:e_z & F_z }$	通常基底の内積に分解
＝右辺

簡略表記

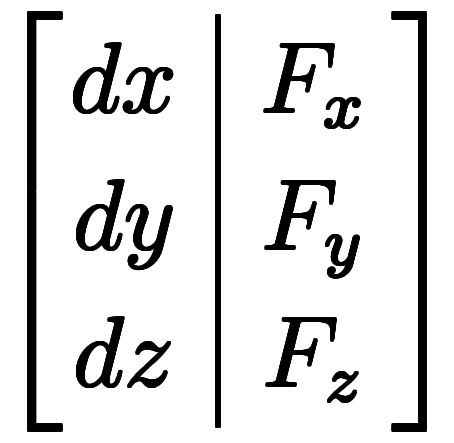
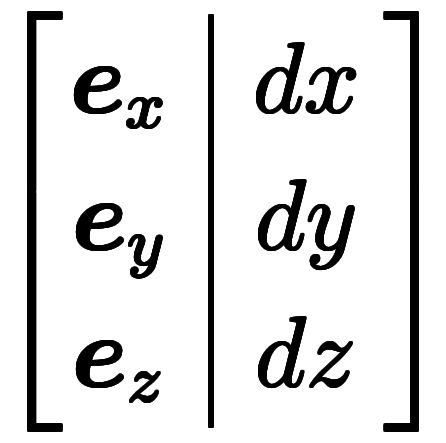
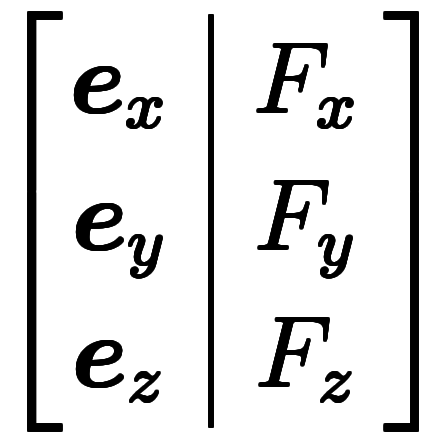上の計算途中で、 $\arrb{ dx & F_x \\ dy & F_y \\ dz & F_z }$ $$ = $$ $\arrb{ \:e_x & dx \\ \:e_y & dy \\ \:e_z & dz }$ $\sx$ $\arrb{ \:e_x & F_x \\ \:e_y & F_y \\ \:e_z & F_z }$ とあるが、注釈にもあるように、微小基底があるために通常基底の内積を取っても３つの項が混ざることはなく、このような割り込みが可能となる。このように、任意のベクトルに対し、通常基底*4を割り込ませ、基底のベクトルと成分のベクトルの内積の形に分解できる。これを利用して $\arrb{\:B & \:C}$ $$ = $$ $\:B \sx \:C$ と定義すれば、通常ベクトルの内積と基底成分表記が簡単に行き来できる。

これより、微小ベクトルの３種類の演算は次のように書ける。

１次形式 $\wx$ ０次形式：　 $[ d\:r | \:A ]$ $\wx$ $[ \spc{ 1}{d\:S} | B\, ]$ $$ = $$ $[ d\:r | \:A B ]$
１次形式 $\wx$ １次形式：　 $[ d\:r | \:A ]$ $\wx$ $[ \spc{d\:r}{d\:S} | \:B ]$ $$ = $$ $[ d\:S | \:A \vx \:B ]$
１次形式 $\wx$ ２次形式：　 $[ d\:r | \:A ]$ $\wx$ $[ \spc{d\:S}{d\:S} | \:B ]$ $$ = $$ $[ d V | \:A \sx \:B ]$

この簡略表記により、ストークスの定理とガウスの定理は次のように変形できる。

$\inte[S] d^{-2}$ $d^2\:S \sx \Big( \ddd{}{\:r} \vx \:F \Big)$	$\inte[S] d^{-2}$ $\arrb{ d^2\:S & \ffd{1}{d\:r} \vx \:F }$	$\inte[R] d^-$ $\arrb{ d\:r & \ffd{1}{d\:r} } \wx \arrb{ d\:r & \:F }$	$\inte[R] d^-$ $\arrb{ d\:r & \:F }$	$\inte[R] d^-$ $d\:r \sx \:F$
$\inte[V] d^{-3}$ $d^3V \Big( \ddd{}{\:r} \sx \:F \Big)$	$\inte[V] d^{-3}$ $\arrb{ d^3V & \ffd{1}{d\:r} \sx \:F }$	$\inte[S] d^{-2}$ $\arrb{ d\:r & \ffd{1}{d\:r} } \wx \arrb{ d^2\:S & \:F }$	$\inte[S] d^{-2}$ $\arrb{ d^2\:S & \:F }$	$\inte[S] d^{-2}$ $d^2\:S \sx \:F$

*4 厳密には双対基底であれば良い。

まとめ・つなぎ

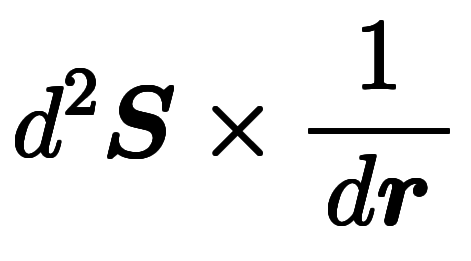
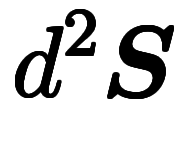今回は、微分形式を経由して、積分公式を導きいた。ベクトル形の積分公式と微分形式を橋渡しするため独自の表記を用いたが、個々の手順自体は合法的。やってることは、 $\arrb{ d^2\:S & \cdots }$ $$ = $$ $\arrb{ d\:r & \cdots } \wx \arrb{ d\:r & \cdots}$ 、 $\arrb{ d^3V & \cdots }$ $$ = $$ $\arrb{ d\:r & \cdots } \wx \arrb{ d\:S & \cdots}$ と微小要素を分解してから、 $\arrb{ d\:r & \ffd{1}{d\:r} }$ 単位で消している。これと同じことを、前回は $d^2\:S \vx \ffd{1}{d\:r}$ $$ = $$ $d\:r$ 、 $\ddd{^3V}{\:r}$ $$ = $$ $d^2\:S$ の形でやっていた。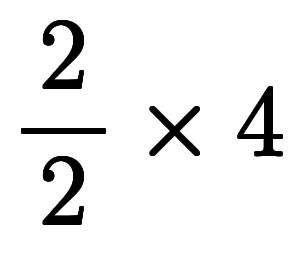直観的には、今回は 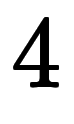$\ffd{8}{2}$ $$ = $$ $\ffd{2}{2} \times 4$ $$ = $$ $$ 4 $$ のように回りくどく因数分解してから約分しているのに対し、前回は 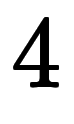$\ffd{8}{2}$ $$ = $$ $$ 4 $$ のように直接割ってる。

また、導入したイカサマ外積も基底側を作るためのものであった。このため、イカサマ外積は必然的に成立していて、必要な演算と言える。というわけで、次回は基底側の計算について考えてみる。

つづき ── 基底積

基底成分表記

最新の20件