多次元フーリエ変換 EditToHeaderToFooter

フーリエ変換は周期現象の記述から制御工学など幅広い分野において役立つ道具である。
空間解析や時空間解析では２次元、３次元、４次元のフーリエ変換が必要となる。
高次元のフーリエ変換では２階の面積分や３階の体積分、４階の多重積分が登場するが、
１階の線積分と紛らわしい表記が通常表記となっている*1*2*3：

正変換：　$$ F(\:k) $$$$ = $$$$ \phantom{\ffd{1}{2\pi}} $$$$ \int_{\mathbb{R}^n}\! $$$$ f(\:r) $$$$ e^{-\:i\,\:k\sx\:r} $$$$ d\:r $$
逆変換：　$$ f(\:r) $$$$ = $$$$ \ffd{1}{(2\pi)^n} $$$$ \int_{\mathbb{R}^n}\! $$$$ F(\:k) $$$$ e^{\:i\,\:k\sx\:r} $$$$ d\:k $$

$$ \:r $$は位置ベクトル
$$ \:k $$は角波数ベクトル、若しくは角空間周波数
$$ \mathbb{R}^n $$は各次元について$$ -\infty $$〜$$ +\infty $$の範囲

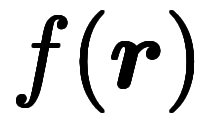
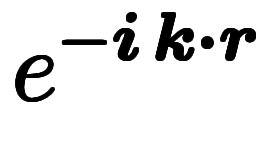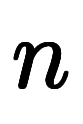例えば、正変換に関して、全領域におけるスカラ場$$ f(\:r) $$$$ e^{-\:i\,\:k\sx\:r} $$の$$ n $$次元線積分が存在するならば、
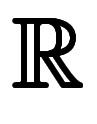積分領域の表記に当たる$$ \mathbb{R}^n $$と$$ \mathbb{R} $$で区別しかない。
それも超体積全領域の意味で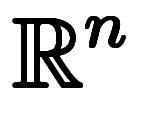$$ \mathrm{V} $$$$ = $$$$ \mathbb{R}^n $$の表記を使うと全くの同形になってしまう。

$$ n $$次元線積分：　$$ \:F(\:k) $$$$ = $$$$ \int_{\mathbb{R}}\! $$$$ f(\:r) $$$$ e^{-\:i\,\:k\sx\:r} $$$$ d\:r $$

$$ n $$次元体積分：　$$ F(\:k) $$$$ = $$$$ \int_{\mathrm{V}}\! $$$$ f(\:r) $$$$ e^{-\:i\,\:k\sx\:r} $$$$ d\:r $$

体積分の表記には微小体積要素$$ dV $$の専用記号を設ける手法が一般的ではあるが、
基底の情報を含まないため、空間領域と角波数領域の区別が求められるフーリエ変換では役不足。

正変換：　$$ F(\:k) $$$$ = $$$$ \phantom{\ffd{1}{2\pi}} $$$$ \int_{\mathbb{R}^3}\! $$$$ f(\:r) $$$$ e^{-\:i\,\:k\sx\:r} $$$$ dV $$

空間領域での微小体積$$ dV $$

逆変換：　$$ f(\:r) $$$$ = $$$$ \ffd{1}{(2\pi)^3} $$$$ \int_{\mathbb{R}^3}\! $$$$ F(\:k) $$$$ e^{\:i\,\:k\sx\:r} $$$$ dV $$

角波数領域での微小体積$$ dV $$

また、空間領域と角波数領域で$$ dV_{\:r} $$や$$ dV_{\:k} $$のように書き分けても、２次元で微小面要素$$ dS_{\:r} $$と$$ dS_{\:k} $$、
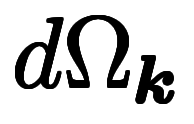４次元で微小超体積要素$$ d\Omega_{\:r} $$と$$ d\Omega_{\:k} $$と場当たり的に記号を増やすことになる。

これに対し、凌宮数学では外積代数に基づく基底積の表記法があり、
基底積を使えば、領域と階数の両方を書き分けできる。

*1 名古屋大学／工学研究科／電子情報システム専攻／中里研究室／固体電子工学／６波の回析と逆格子
*2 中央大学／理工学研究科／物理学専攻／中野研究室／数理解析／２フーリエ変換
*3 太字のベクトル$$ d\:r $$に対応した細字のスカラの$$ dr $$で記述する流派もあるが、工学一般で暗黙に使われる弧長積分$$ dr $$$$ = $$$$ |d\:r| $$と紛らわしくなる。

基底積による多次元フーリエ変換の記述 EditToHeaderToFooter

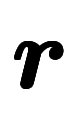位置ベクトル$$ \:r $$に対し、微小変位ベクトル$$ d\:r $$が定義でき、
各次元における最高階のウェッジ積は全成分の積なる。

１次元

$$ d\:r $$$$ = $$$$ (dx) $$

$$ d\:r^{\wx1} $$$$ = $$$$ dx $$

２次元

$$ d\:r $$$$ = $$$$ (dx, dy) $$

$$ d\:r^{\wx2} $$$$ = $$$$ dx $$$$ dy $$

３次元

$$ d\:r $$$$ = $$$$ (dx, dy, dz) $$

$$ d\:r^{\wx3} $$$$ = $$$$ dx $$$$ dy $$$$ dz $$

４次元

$$ d\:r $$$$ = $$$$ (dx, dy, dz, dt) $$

$$ d\:r^{\wx4} $$$$ = $$$$ dx $$$$ dy $$$$ dz $$$$ dt $$

同様に角波数ベクトル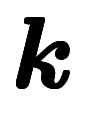$$ \:k $$に対し、微小角波数ベクトル$$ d\:k $$が定義でき、
各次元におけるウェッジ積により最高次数のウェッジ積は以下のようになる。

１次元

$$ d\:k $$$$ = $$$$ (dk_x) $$

$$ d\:k^{\wx1} $$$$ = $$$$ dk_x $$

２次元

$$ d\:k $$$$ = $$$$ (dk_x, dk_y) $$

$$ d\:k^{\wx2} $$$$ = $$$$ dk_x $$$$ dk_y $$

３次元

$$ d\:k $$$$ = $$$$ (dk_x, dk_y, dk_z) $$

$$ d\:k^{\wx3} $$$$ = $$$$ dk_x $$$$ dk_y $$$$ dk_z $$

４次元

$$ d\:k $$$$ = $$$$ (dk_x, dk_y, dk_z, d\omega) $$

$$ d\:k^{\wx4} $$$$ = $$$$ dk_x $$$$ dk_y $$$$ dk_z $$$$ d\omega $$

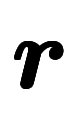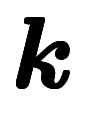基底積の表記には、空間を表す基底$$ \:r $$と$$ \:k $$を含むため、空間を書き分けできる。
また、微小の次数を含むため、線積分とも書き分けできる。

基底積を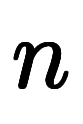$$ n $$次元のフーリエ変換に適応すると、以下のようになる：

正変換：　$$ F(\:k) $$$$ = $$$$ \phantom{\ffd{1}{2\pi}} $$$$ \int_{\mathbb{R}^n}\! $$$$ f(\:r) $$$$ e^{-\:i \:k\sx\:r} $$$$ d\:r^{\wx n} $$
逆変換：　$$ f(\:r) $$$$ = $$$$ \ffd{1}{(2\pi)^n} $$$$ \int_{\mathbb{R}^n}\! $$$$ F(\:k) $$$$ e^{\:i \:k\sx\:r} $$$$ d\:k^{\wx n} $$

$$ \:r $$は位置ベクトル
$$ \:k $$は角波数ベクトル

特に、４次元時空間領域でのフーリエ変換に対し、基底部の成分表示で柔軟に記述できる。

正変換：　$$ F(\:k, \omega) $$$$ = $$$$ \phantom{\ffd{1}{2\pi}} $$$$ \int_{\mathbb{R}^4}\! $$$$ f(\:r, t) $$$$ e^{-\:i (\:k\sx\:r - \omega t)} $$$$ d(\:r, t)^{\wx 4} $$
逆変換：　$$ f(\:r, t) $$$$ = $$$$ \ffd{1}{(2\pi)^4} $$$$ \int_{\mathbb{R}^4}\! $$$$ F(\:k, \omega) $$$$ e^{\:i (\:k\sx\:r - \omega t)} $$$$ d(\:k, \omega)^{\wx 4} $$

$$ \:r $$は位置ベクトル
$$ \:k $$は角波数ベクトル
$$ t $$は時刻
$$ \omega $$は角周波数
    数学 一覧 検索 最新 バックアップ リンク元   ヘルプ   最終更新のRSS