![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
定数係数1階線形常微分方程式 のバックアップの現在との差分(No.14) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
定数係数1階線形常微分方程式 のバックアップの現在との差分(No.14) |
|
|
|
 階の定数係数常微分方程式に繋がるような、
階の定数係数常微分方程式に繋がるような、

 とする演算子法では、逆演算子
とする演算子法では、逆演算子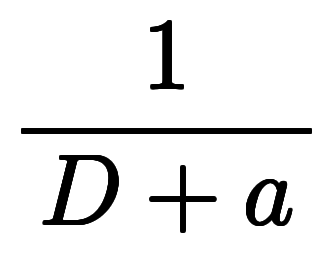 の形で暗記対象になる*4:
の形で暗記対象になる*4:    ⇔ ⇔      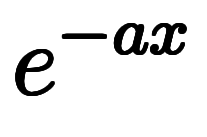     |
 を導入して、
を導入して、 の
の に単純な意味を与え、
に単純な意味を与え、     |
⇔ 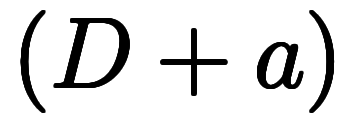  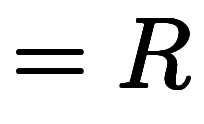 |
⇔       |
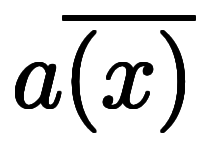 は凌宮数学の定数表記であり、
は凌宮数学の定数表記であり、

 を表す。
を表す。




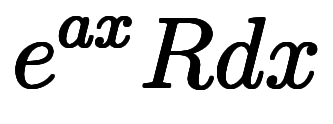


 と積分定数を明示する書き方もあるが、煩雑のため凌宮数学では使わない。
と積分定数を明示する書き方もあるが、煩雑のため凌宮数学では使わない。 の分解表記
の分解表記 


 の逆演算子
の逆演算子 





 に対し、不定積分
に対し、不定積分



 が定義される。
が定義される。 の逆演算
の逆演算 は不定積分
は不定積分 〜
〜 となる。
となる。


 ⇔
⇔ 

 *5
*5 


 の場合は、左辺
の場合は、左辺

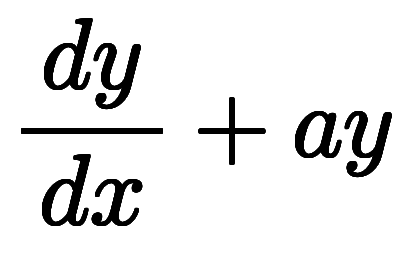 を
を に纏めらると、積分で解ける。
に纏めらると、積分で解ける。
 の分解表記
の分解表記 


 の特徴は、「
の特徴は、「 」、「
」、「 」、「加算」である。
」、「加算」である。 で書き換えると:
で書き換えると: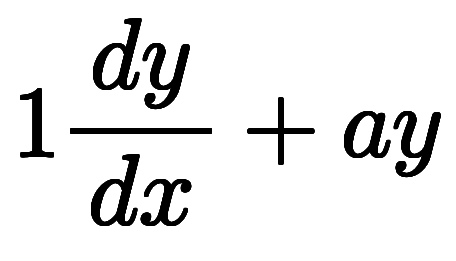 として
として



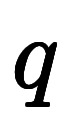 と比較すると、
と比較すると、  が上手く嵌るものの、
が上手く嵌るものの、

 と
と

 を同時に満たす
を同時に満たす は存在しない*7。
は存在しない*7。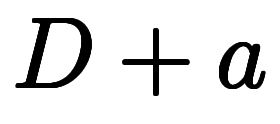 の逆演算子である
の逆演算子である は形式的に次のように分解できる:
は形式的に次のように分解できる:  ![\iro[ao]{e^{-ax}} $$ \iro[ao]{e^{-ax}} $$](./eq/eq-ni-0e76f663d74e5eecabef3ffff2a2f021.png)  ![(\iro[ao]{e^{ax}} \ast) $$ (\iro[ao]{e^{ax}} \ast) $$](./eq/eq-ni-5b2a0cc5afed36fd3c2ca67167727aa0.png) |
 と書いている箇所に
と書いている箇所に が入るが、これを簡単に省けない。
が入るが、これを簡単に省けない。 は
は と
と の両方に掛かるが、
の両方に掛かるが、
 と書いた場合は
と書いた場合は だけの積分に化けてしまう。
だけの積分に化けてしまう。 も演算子にする必要がある。
も演算子にする必要がある。








 と指数変換演算子を定義すると、
と指数変換演算子を定義すると、 は必ず何かに作用し、
は必ず何かに作用し、
 だけで
だけで
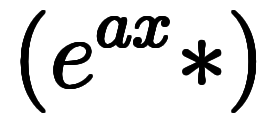 を表現できるようになる。
を表現できるようになる。 を使えば、
を使えば、 は
は と
と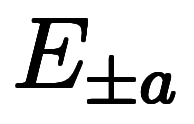 の演算子チェーンとして記述できる:
の演算子チェーンとして記述できる: ⇒ ⇒ ![\iro[ao]{E_{-a}} $$ \iro[ao]{E_{-a}} $$](./eq/eq-ni-b1bcf017339306e22c534fb8353ac6f1.png)  ![\iro[ao]{E_a} $$ \iro[ao]{E_a} $$](./eq/eq-ni-47bf98cede895b392b1218d719b3904d.png) |
 は
は の掛算であるため、逆演算子
の掛算であるため、逆演算子 は
は の逆数の掛算となる:
の逆数の掛算となる:  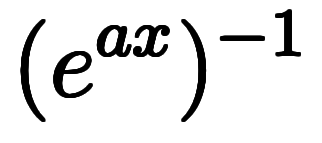    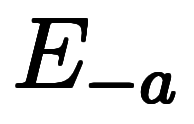 |
 は
は と
と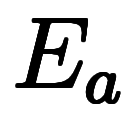 だけの演算子チェーンとして記述できる:
だけの演算子チェーンとして記述できる: ⇒ ⇒ ![\iro[ao]{E_a^{-1}} $$ \iro[ao]{E_a^{-1}} $$](./eq/eq-ni-b26d0ab6a086c42bf8a66d43c9ab44fd.png)  ![\iro[ao]{E_a} $$ \iro[ao]{E_a} $$](./eq/eq-ni-47bf98cede895b392b1218d719b3904d.png) |
 で指数変換してから、積分して、
で指数変換してから、積分して、 の逆変換を掛ける、と読める。
の逆変換を掛ける、と読める。







 のままでは1つの微分に纏まらないため、これを弄ることになる。
のままでは1つの微分に纏まらないため、これを弄ることになる。 が入ると積分できなくなるため、右辺を
が入ると積分できなくなるため、右辺を の関数に保たせる必要がある。
の関数に保たせる必要がある。
 の分解表記
の分解表記 


 の係数が
の係数が である故に
である故に

 と決まってしまうため、
と決まってしまうため、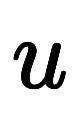

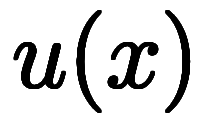 を掛けてみると、1つの微分に纏まりそうな
を掛けてみると、1つの微分に纏まりそうな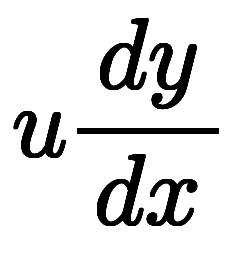

 が現れる。
が現れる。 は積分因子と呼ばれ、微分の形が変わるため積分因子を掛ける手法は良く利く。
は積分因子と呼ばれ、微分の形が変わるため積分因子を掛ける手法は良く利く。

 の逆演算を取ると、
の逆演算を取ると、 が得られる:
が得られる: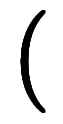    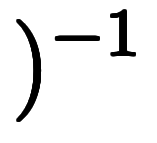 | |
= 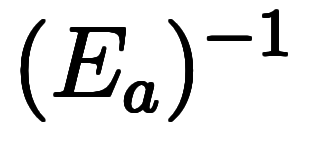 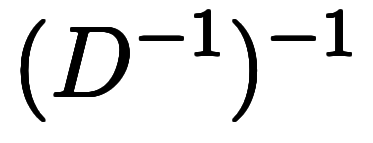 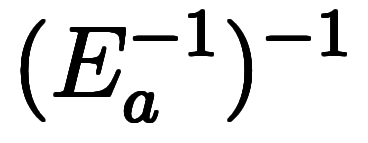 | チェーンの逆演算は、各演算子の逆演算を逆順に並び*8 |
=    | 逆演算の逆演算は正演算 |
 で指数変換してから、微分し、逆変換を掛ける、と読める。
で指数変換してから、微分し、逆変換を掛ける、と読める。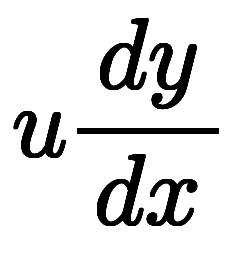

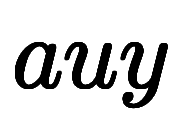 を
を



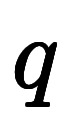 と比較すると、
と比較すると、 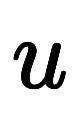

 と
と

 が得られる。
が得られる。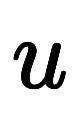

 を
を

 に代入すれば変数分離形という易しい微分方程式が得られる:
に代入すれば変数分離形という易しい微分方程式が得られる: が正演算に戻るだけで、
が正演算に戻るだけで、 と
と に関しては変わりが無い。
に関しては変わりが無い。 | 指数変換→微分→逆変換 |
⇔ | 変数分離 指数変換→積分→逆変換 |



⇔ | |
⇔ 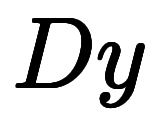     | 両辺で不定積分 式1:常微分演算子表記 |
⇔ | 不定積分実行、積分定数を |
⇔ | 両辺で指数を取る 式3:演算子分解 |
⇔ | 指数法則で定数部を分離 式4:逆演算子表記 |
⇔   ![\iro[ao]{e^{-ax}} \!\!\int\!\! \iro[ao]{e^{ax}} $$ \iro[ao]{e^{-ax}} \!\!\int\!\! \iro[ao]{e^{ax}} $$](./eq/eq-ni-0a0a88d360569cf362cf0d5875cb8d78.png)   | 式5:通常表記に復元 |
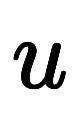

 を選ぶ。
を選ぶ。






 だけを逆演算子に書き換えると式3’が得られる:
だけを逆演算子に書き換えると式3’が得られる: | 原方程式 式2 |
⇔ | 両辺に積分因子 |
 と
と に関する定数係数1階線形常微方程式は、
に関する定数係数1階線形常微方程式は、
 と
と
 に関する定数項無しの微分方程式であると解釈できる。この考え方に基づくと、解答は次のように変る。
に関する定数項無しの微分方程式であると解釈できる。この考え方に基づくと、解答は次のように変る。 ⇔ | |
⇔ 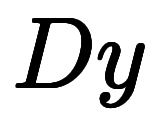     | 指数の微分を逆適応(不定積分を実行) 式1:常微分演算子表記 |
⇔ | 積の微分を逆適応(部分積分を実行) 式2:定数係数1階線形常微分演算子表記 |
⇔ | 微分・不定積分の相互変換 式3’:定数係数無しの微分方程式に読み替え |
⇔ | 両辺に |
⇔   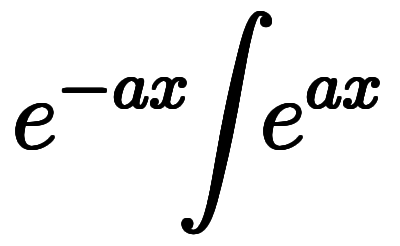   | 式5:通常表記に復元 |





 と置けば1階線形常微分方程式を
と置けば1階線形常微分方程式を


 に書き換えるのは容易だろう。
に書き換えるのは容易だろう。






 と答えを丸暗記するよりは、
と答えを丸暗記するよりは、




 と分解してから個別に逆演算に直す方が覚えやすく、
と分解してから個別に逆演算に直す方が覚えやすく、




 と両辺の指数変換
と両辺の指数変換 を経ての
を経ての と覚える方が理屈を付けやすいだろう。
と覚える方が理屈を付けやすいだろう。 に対し
に対し と
と しか登場しなければ、
しか登場しなければ、 と
と の順番を覚える必要が無くなる。
の順番を覚える必要が無くなる。