![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
定数係数1階線形常微分方程式 |
凌宮読取術: |
|
定数係数の1階線形常微分方程式は微分で定義される多くの分野で現れるため、
「変数分離法&定数変化法」*1という定番解法が大学入学早々叩き込まれる。
変数分離法と定数変化法では解けることができても、直観的に解を得るのは難しい。
その上、高階の方程式を解くのに1階の解が多用されるため、ほぼ丸暗記する羽目になる。
例えば

 とする演算子法では、逆演算子
とする演算子法では、逆演算子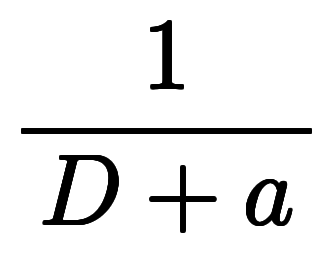 の形で暗記対象になる*2:
の形で暗記対象になる*2:
|
これに対し、凌宮数学では直観を重視する演算子法を拡張し、
指数変換演算子 を導入して、
を導入して、 の
の に単純な意味を与え、
に単純な意味を与え、
高階の常微分方程式に繋げやすい解法を与える。
|
⇔ |
⇔ |
 の分解表記
の分解表記 


 の逆演算子
の逆演算子 


一般に、微分


 に対し、不定積分
に対し、不定積分



 が定義される。
が定義される。
このため、微分演算 の逆演算
の逆演算 は不定積分
は不定積分 〜
〜 となる。
となる。
 の分解表記
の分解表記 


定数係数の1階線形常微分方程式とその解の公式の積分を で書き換えると:
で書き換えると:
|
このため、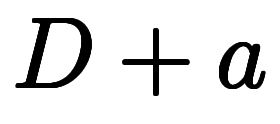 の逆演算子である
の逆演算子である は形式的に次のように分解できる:
は形式的に次のように分解できる:
|
問題は、 と書いている箇所に
と書いている箇所に が入るが、これを簡単に省けない。
が入るが、これを簡単に省けない。
 は
は と
と の両方に掛かるが、
の両方に掛かるが、
 と書いた場合は
と書いた場合は だけの積分に化けてしまう。
だけの積分に化けてしまう。
このため、積分対象を簡潔にかつ正しく記述するには、 も演算子にする必要がある。
も演算子にする必要がある。








 と指数変換演算子を定義すると、
と指数変換演算子を定義すると、
 は必ず何かに作用し、
は必ず何かに作用し、
 だけで
だけで
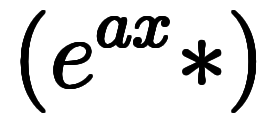 を表現できるようになる。
を表現できるようになる。
 を使えば、
を使えば、 は
は と
と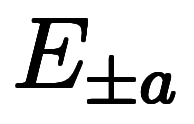 の演算子チェーンとして記述できる:
の演算子チェーンとして記述できる:
|
さらに、 は
は の掛算であるため、逆演算子
の掛算であるため、逆演算子 は
は の逆数の掛算となる:
の逆数の掛算となる:
|
これを利用すれば、 は
は と
と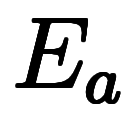 だけの演算子チェーンとして記述できる:
だけの演算子チェーンとして記述できる:
|
意味は、 で指数変換してから、積分して、
で指数変換してから、積分して、 の逆変換を掛ける、と読める。
の逆変換を掛ける、と読める。
 の分解表記
の分解表記 




 の逆演算を取ると、
の逆演算を取ると、 が得られる:
が得られる:
| |
= | チェーンの逆演算は、各演算子の逆演算を逆順に並び*3 |
= | 逆演算の逆演算は正演算 |
意味は、 で指数変換してから、微分し、逆変換を掛ける、と読める。
で指数変換してから、微分し、逆変換を掛ける、と読める。
ポイントは が正演算に戻るだけで、
が正演算に戻るだけで、 と
と に関しては変わりが無い。
に関しては変わりが無い。
| 指数変換→微分→逆変換 |
| 指数変換→積分→逆変換 |



以上を纏めると、演算子分解法を使えば、定数係数1階数線形常微分方程式を以下のように解ける:
| |
⇔ | 式1:常微分演算子表記 |
⇔ | 式2:定数係数1階線形常微分演算子表記 |
⇔ | 式3:演算子分解 |
⇔ | 式4:逆演算子表記 |
⇔ | 式5:通常表記に復元 |



上記式3を式4に書き換える途中、先頭の だけを逆演算子に書き換えると式3’が得られる:
だけを逆演算子に書き換えると式3’が得られる:
| 式2 |
⇔ | 式3’: |
式2と式3'を見比べれば、 と
と に関する定数係数1階線形常微方程式は、
に関する定数係数1階線形常微方程式は、
指数変換を施した
 と
と
 に関する定数項無しの微分方程式であると解釈できる。
に関する定数項無しの微分方程式であると解釈できる。
この考え方に基づくと、解答は次のように変る。
| |
⇔ | 式1:常微分演算子表記 |
⇔ | 式2:定数係数1階線形常微分演算子表記 |
⇔ | 式3’:定数係数無しの微分方程式に読み替え |
⇔ | 式4:逆演算子表記 |
⇔ | 式5:通常表記に復元 |





 と置けば1階線形常微分方程式を
と置けば1階線形常微分方程式を


 に書き換えるのは容易だろう。
に書き換えるのは容易だろう。
その先、


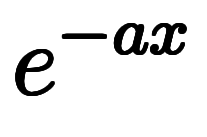



 と答えを丸暗記するよりは、
と答えを丸暗記するよりは、
段階的に




 と分解してから個別に逆演算に直す方が覚えやすく、
と分解してから個別に逆演算に直す方が覚えやすく、





 と両辺の指数変換
と両辺の指数変換 を経ての
を経ての と覚える方が理屈を付けやすいだろう。
と覚える方が理屈を付けやすいだろう。
 に対し
に対し と
と しか登場しなければ、
しか登場しなければ、 と
と の順番を覚える必要が無くなる。
の順番を覚える必要が無くなる。
小さいことではあるが、片方に付くが他方に付かない「-1」などは、混乱の元でしか無い。