![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
定数係数1階線形常微分方程式 のバックアップの現在との差分(No.22) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
定数係数1階線形常微分方程式 のバックアップの現在との差分(No.22) |
|
|
|
 階の定数係数常微分方程式に繋がるような、
階の定数係数常微分方程式に繋がるような、

 とする演算子法では、逆演算子
とする演算子法では、逆演算子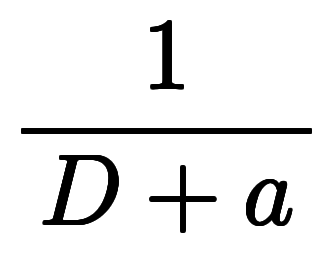 の形で暗記対象になる*4:
の形で暗記対象になる*4:    ⇔ ⇔      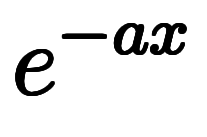     |
 を導入して、
を導入して、 の
の に単純な意味を与え、
に単純な意味を与え、     |
⇔ 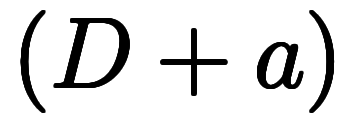  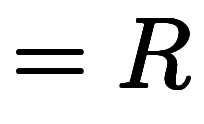 |
⇔       |
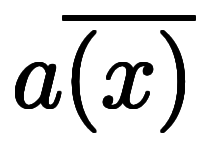 は凌宮数学の定数表記であり、
は凌宮数学の定数表記であり、

 を表す。
を表す。




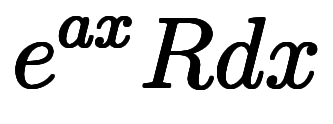


 と積分定数を明示する書き方もあるが、煩雑のため凌宮数学では使わない。
と積分定数を明示する書き方もあるが、煩雑のため凌宮数学では使わない。 の分解表記
の分解表記 


 の逆演算子
の逆演算子 





 に対し、不定積分
に対し、不定積分



 が定義される。
が定義される。 の逆演算
の逆演算 は不定積分
は不定積分 〜
〜 となる。
となる。






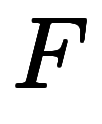 の常微分が分かれば、不定積分で解ける。
の常微分が分かれば、不定積分で解ける。
 の分解表記
の分解表記 


 で書き換えると:
で書き換えると: |




 の場合は、左辺
の場合は、左辺

 を
を に纏めらると、積分で解ける。
に纏めらると、積分で解ける。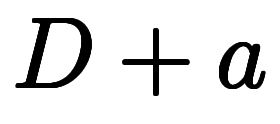 の逆演算子である
の逆演算子である は形式的に次のように分解できる:
は形式的に次のように分解できる:  ![\iro[ao]{e^{-ax}} $$ \iro[ao]{e^{-ax}} $$](./eq/eq-ni-0e76f663d74e5eecabef3ffff2a2f021.png)  ![(\iro[ao]{e^{ax}} \ast) $$ (\iro[ao]{e^{ax}} \ast) $$](./eq/eq-ni-5b2a0cc5afed36fd3c2ca67167727aa0.png) |
 と書いている箇所に
と書いている箇所に が入るが、これを簡単に省けない。
が入るが、これを簡単に省けない。 は
は と
と の両方に掛かるが、
の両方に掛かるが、
 と書いた場合は
と書いた場合は だけの積分に化けてしまう。
だけの積分に化けてしまう。 も演算子にする必要がある。
も演算子にする必要がある。











 の特徴は、「
の特徴は、「 」、「
」、「 」、「
」、「 」である。
」である。

 と指数変換演算子を定義すると、
と指数変換演算子を定義すると、 は必ず何かに作用し、
は必ず何かに作用し、
 だけで
だけで
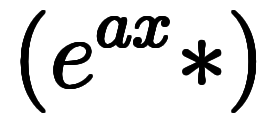 を表現できるようになる。
を表現できるようになる。 を使えば、
を使えば、 は
は と
と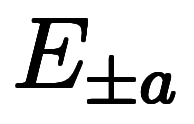 の演算子チェーンとして記述できる:
の演算子チェーンとして記述できる: |




 を
を

 と比較しても、
と比較しても、

 が嵌るものの、
が嵌るものの、

 と
と

 を同時に満せない。
を同時に満せない。

 を弄る必要がある。
を弄る必要がある。 は
は の掛算であるため、逆演算子
の掛算であるため、逆演算子 は
は の逆数の掛算となる:
の逆数の掛算となる:  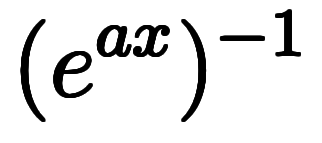    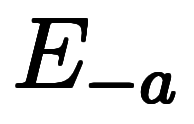 |





 の縛りが厳しすぎるため、
の縛りが厳しすぎるため、

 となってしまい、
となってしまい、

 を満たす余地を無くしている。
を満たす余地を無くしている。 をそのまま
をそのまま



 の両辺に掛ければ叶える:これを利用すれば、
の両辺に掛ければ叶える:これを利用すれば、 は
は と
と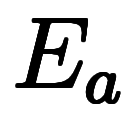 だけの演算子チェーンとして記述できる:
だけの演算子チェーンとして記述できる: |
 を積分因子と呼ぶ。
を積分因子と呼ぶ。 で指数変換してから、積分して、
で指数変換してから、積分して、 の逆変換を掛ける、と読める。
の逆変換を掛ける、と読める。


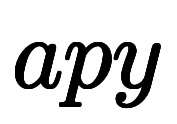

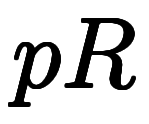 を
を



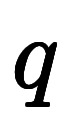 と比較すると、
と比較すると、 

 なる
なる を探せば良いことが分かる。
を探せば良いことが分かる。 の分解表記
の分解表記 




 の逆演算を取ると、
の逆演算を取ると、 が得られる:
が得られる: | 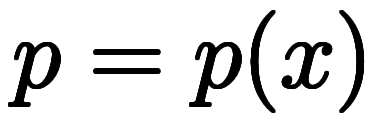 に関する変数分離形の常微分方程式 に関する変数分離形の常微分方程式     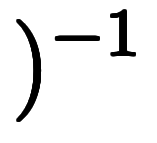 |
⇔ | 変数分離 チェーンの逆演算は、各演算子の逆演算を逆順に並び *7 |
⇔ | 不定積分 逆演算の逆演算は正演算 |
 で指数変換してから、微分し、逆変換を掛ける、と読める。
で指数変換してから、微分し、逆変換を掛ける、と読める。 が正演算に戻るだけで、
が正演算に戻るだけで、 と
と に関しては変わりが無い。
に関しては変わりが無い。 ⇔ | 積分実行、積分定数を |
⇔ | 両辺で指数を取る |
⇔     | 指数法則で定数部を分離 指数変換→積分→逆変換 |
 は
は
 を満たせば良いので、以降では簡単そうな
を満たせば良いので、以降では簡単そうな を選ぶ。
を選ぶ。






| 原方程式 |
⇔ | 両辺に積分因子 |
⇔ | 積の微分に嵌める(不定積分を実行) 式2:定数係数1階線形常微分演算子表記 |
⇔ | 1つの微分に纏める(部分積分を実行) 式3:演算子分解 |
⇔ | 積分する 式4:逆演算子表記 |
⇔ | 両辺に |



 は、未知関数
は、未知関数 から既知関数
から既知関数 を求める複雑な微分演算にも見える。
を求める複雑な微分演算にも見える。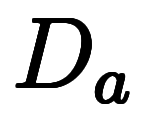 を定義すると、演算
を定義すると、演算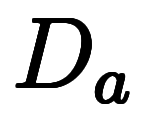 と演算対象
と演算対象 に明示的に分離できる。
に明示的に分離できる。



 だけを逆演算子に書き換えると式3’が得られる:
だけを逆演算子に書き換えると式3’が得られる: 1階線形常微分演算子: | 式2 |
1階線形常微分方程式: | 式3’:  のみを逆演算子に書き換えた状態 のみを逆演算子に書き換えた状態 |
 と
と に関する定数係数1階線形常微方程式は、
に関する定数係数1階線形常微方程式は、
 と
と
 に関する定数項無しの微分方程式であると解釈できる。
に関する定数項無しの微分方程式であると解釈できる。 と
と では単純な微分・積分の関係にならないため、
では単純な微分・積分の関係にならないため、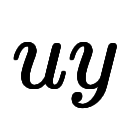

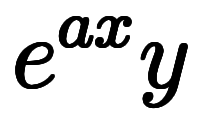 と
と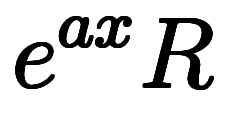 に変換してから、単純な微分を単純な積分に直している。
に変換してから、単純な微分を単純な積分に直している。 と
と に関する一対の複雑な微分と積分にも見える:この考え方に基づくと、解答は次のように変る。
に関する一対の複雑な微分と積分にも見える:この考え方に基づくと、解答は次のように変る。     | |
⇔ 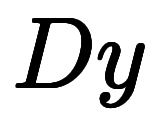     | 式1:常微分演算子表記 |
⇔     | 式2:定数係数1階線形常微分演算子表記 |
⇔       | 式3’:定数係数無しの微分方程式に読み替え |
⇔       | 式4:逆演算子表記 |
⇔   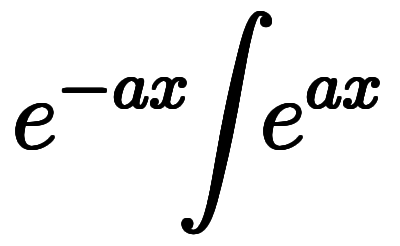   | 式5:通常表記に復元 |




 が
が から
から への複雑な微分
への複雑な微分





 は
は から
から への複雑な積分
への複雑な積分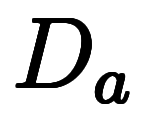 を
を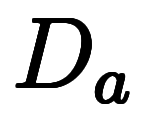






 と定義し、
と定義し、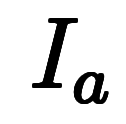 を
を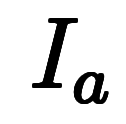






 と定義すると、
と定義すると、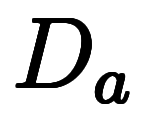
![\iro[gy]y $$ \iro[gy]y $$](./eq/eq-ni-48d32a2569f09f042196c7ad3e4b5898.png)

![\iro[gy]R $$ \iro[gy]R $$](./eq/eq-ni-2d930a54fd3cb219703755c888a54f90.png) ⇔
⇔ ![\iro[gy]y $$ \iro[gy]y $$](./eq/eq-ni-48d32a2569f09f042196c7ad3e4b5898.png)

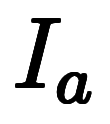
![\iro[gy]R $$ \iro[gy]R $$](./eq/eq-ni-2d930a54fd3cb219703755c888a54f90.png)
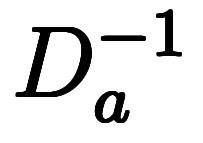

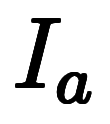








 と置けば1階線形常微分方程式を
と置けば1階線形常微分方程式を


 に書き換えるのは容易だろう。
に書き換えるのは容易だろう。






 と答えを丸暗記するよりは、
と答えを丸暗記するよりは、




 と分解してから個別に逆演算に直す方が覚えやすく、
と分解してから個別に逆演算に直す方が覚えやすく、




 と両辺の指数変換
と両辺の指数変換 を経ての
を経ての と覚える方が理屈を付けやすいだろう。
と覚える方が理屈を付けやすいだろう。 に対し
に対し と
と しか登場しなければ、
しか登場しなければ、 と
と の順番を覚える必要が無くなる。
の順番を覚える必要が無くなる。