![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
定数係数1階線形常微分方程式 のバックアップの現在との差分(No.26) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
定数係数1階線形常微分方程式 のバックアップの現在との差分(No.26) |
【簡略中】凌宮読取術:
|
|


 による演算子法が工学で多用される*1:
による演算子法が工学で多用される*1:

 とする演算子法では、逆演算子
とする演算子法では、逆演算子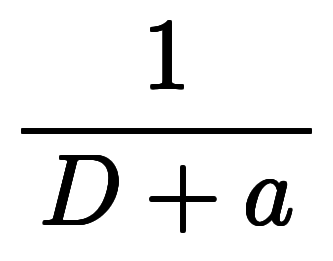 の形で暗記対象になる*3:
の形で暗記対象になる*3: |
 を導入して、
を導入して、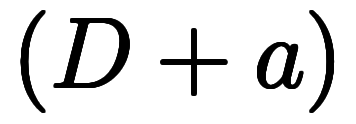 の
の に単純な意味を与え、
に単純な意味を与え、 |
⇔ 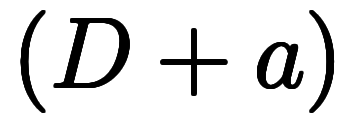  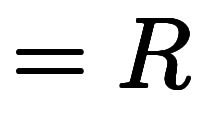 |
⇔       |
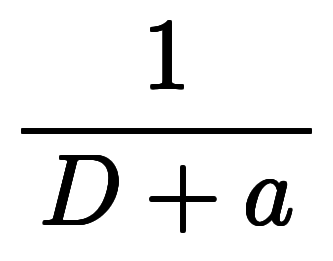 は暗記対象になるが、
は暗記対象になるが、 を更に分解し、
を更に分解し、 が一般的な表記ではあるが、高階微分方程式の解法として部分分数分解を続けて使う文脈では分数型
が一般的な表記ではあるが、高階微分方程式の解法として部分分数分解を続けて使う文脈では分数型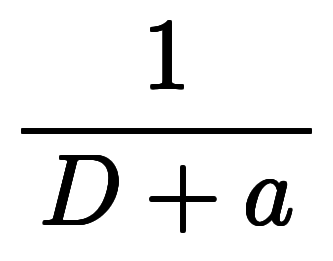 とも表記される。
とも表記される。


 の分解表記
の分解表記 


 の逆演算子
の逆演算子 


 の逆演算子
の逆演算子 


一般に、微分


 に対し、不定積分
に対し、不定積分



 が定義される。
が定義される。
このため、微分演算 の逆演算
の逆演算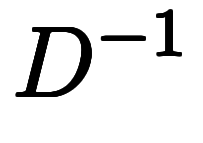 は不定積分
は不定積分 〜
〜 となる。
となる。
 の分解表記
の分解表記 


 の分解表記
の分解表記 


定数係数の1階線形常微分方程式とその解の公式の積分を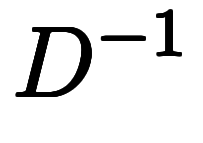 で書き換えると:
で書き換えると:
|
このため、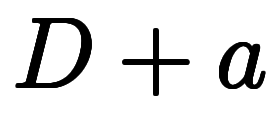 の逆演算子である
の逆演算子である は形式的に次のように分解できる:
は形式的に次のように分解できる:
|
 と書いている箇所に作用対象が入る。
と書いている箇所に作用対象が入る。 と
と の作用対象である
の作用対象である の両方が
の両方が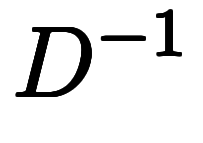 の積分対象に入るのがポイントである。
の積分対象に入るのがポイントである。 を抜いて、単に
を抜いて、単に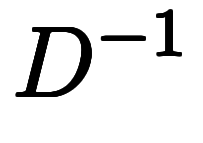
 と書くと、
と書くと、 だけの積分に化けてしまう。
だけの積分に化けてしまう。 も演算子にする必要がある。
も演算子にする必要がある。 と書いている箇所に
と書いている箇所に が入るが、これを簡単に省けない。
が入るが、これを簡単に省けない。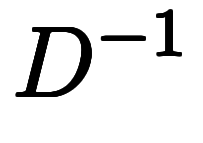 は
は と
と の両方に掛かるが、
の両方に掛かるが、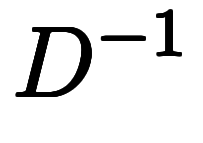
 と書いた場合は
と書いた場合は だけの積分に化けてしまう。
だけの積分に化けてしまう。 も演算子にする必要がある。
も演算子にする必要がある。














 と指数変換演算子を定義すると、
と指数変換演算子を定義すると、 は必ず何かに作用し、
は必ず何かに作用し、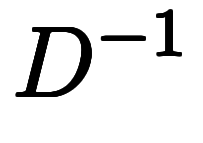
 だけで
だけで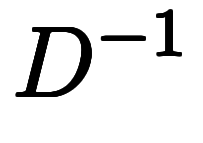
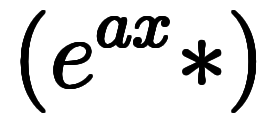 を表現できるようになる。
を表現できるようになる。 を使えば、
を使えば、 は
は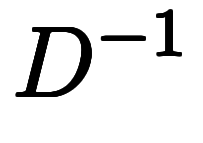 と
と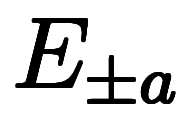 の演算子チェーンとして記述できる:
の演算子チェーンとして記述できる: |
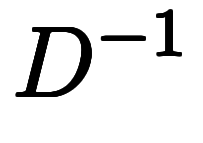
 だけで
だけで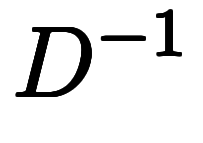
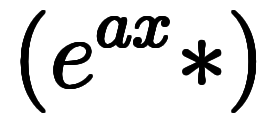 を意味する。すると、
を意味する。すると、 は
は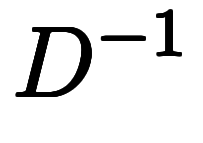 と
と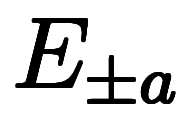 の演算子チェーンとして記述できる:
の演算子チェーンとして記述できる: ⇒ ⇒ 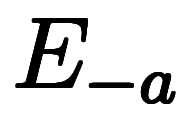 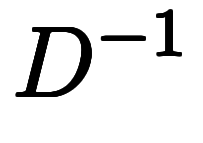  |
 は
は の掛算であるため、逆演算子
の掛算であるため、逆演算子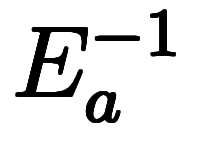 は
は の逆数の掛算となる:
の逆数の掛算となる: |
これを利用すれば、 は
は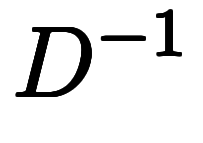 と
と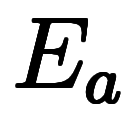 だけの演算子チェーンとして記述できる:
だけの演算子チェーンとして記述できる:
|
 で変換してから、積分して、逆変換を掛ける、と読める。
で変換してから、積分して、逆変換を掛ける、と読める。 で指数変換してから、積分して、
で指数変換してから、積分して、 の逆変換を掛ける、と読める。
の逆変換を掛ける、と読める。
 の分解表記
の分解表記 


 の分解表記
の分解表記 


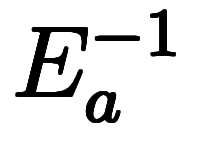
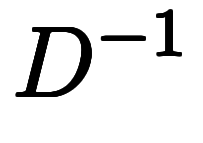
 の逆演算を取ると、
の逆演算を取ると、 が得られる:
が得られる:
| |
= | 演算子チェーンの逆演算は、各演算子の逆演算を逆順に並び チェーンの逆演算は、各演算子の逆演算を逆順に並び *4 |
= | 逆演算の逆演算は正演算 |
 で指数変換してから、微分し、逆変換を掛ける、と読める。
で指数変換してから、微分し、逆変換を掛ける、と読める。ポイントは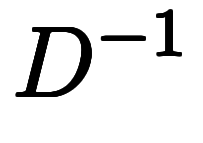 が正演算に戻るだけで、
が正演算に戻るだけで、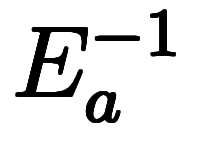 と
と に関しては変わりが無い。
に関しては変わりが無い。
| 指数変換→微分→逆変換 |
  ![\iro[ao]{E_a^{-1}} $$ \iro[ao]{E_a^{-1}} $$](./eq/eq-ni-b26d0ab6a086c42bf8a66d43c9ab44fd.png) 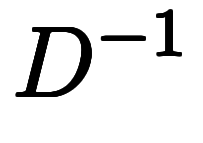 ![\iro[ao]{E_a} $$ \iro[ao]{E_a} $$](./eq/eq-ni-47bf98cede895b392b1218d719b3904d.png) | 指数変換→積分→逆変換 |
 で指数変換してから、微分し、逆変換を掛ける、と読める。
で指数変換してから、微分し、逆変換を掛ける、と読める。






| |
⇔ | 式1:常微分演算子表記 |
⇔ | 式2:定数係数1階線形常微分演算子表記 |
⇔ | 式3:演算子分解 |
⇔ | 式4:逆演算子表記 |
⇔ | 式5:通常表記に復元 |






上記式3を式4に書き換える途中、先頭の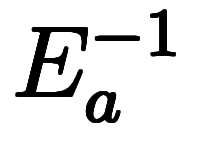 だけを逆演算子に書き換えると式3’が得られる:
だけを逆演算子に書き換えると式3’が得られる:
| 式2 |
⇔ | 式3’: |
作用対象  と作用結果 と作用結果 に対する定数係数1階線形常微分演算 に対する定数係数1階線形常微分演算 は、 は、 両方に指数変換演算  を施してからの常微分演算 を施してからの常微分演算 と等価である。 と等価である。 |
 と
と に関する定数係数1階線形常微方程式は、
に関する定数係数1階線形常微方程式は、
 と
と
 に関する定数項無しの微分方程式であると解釈できる。このため、次の考え方に基づく解答も可能である。この考え方に基づくと、解答は次のように変る。
に関する定数項無しの微分方程式であると解釈できる。このため、次の考え方に基づく解答も可能である。この考え方に基づくと、解答は次のように変る。
| |
⇔ | 式1:常微分演算子表記 |
⇔ | 式2:定数係数1階線形常微分演算子表記 |
⇔ | 式3’:両辺に対する指数変換を経ての常微分演算に分解 式3’:定数係数無しの微分方程式に読み替え |
⇔ | 式4:逆演算子表記 |
⇔ | 式5:通常表記に復元 |








 と置けば1階線形常微分方程式を
と置けば1階線形常微分方程式を


 に書き換えるのは容易であろう。
に書き換えるのは容易であろう。

 と置けば1階線形常微分方程式を
と置けば1階線形常微分方程式を


 に書き換えるのは容易だろう。
に書き換えるのは容易だろう。


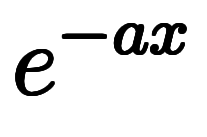



 と答えを丸暗記するよりは、
と答えを丸暗記するよりは、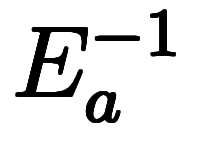




 と一旦分解してから個別に逆演算に直す方が理屈を付け易く、
と一旦分解してから個別に逆演算に直す方が理屈を付け易く、




 と両辺の指数変換
と両辺の指数変換 を経ての
を経ての と覚える方が容易である。
と覚える方が容易である。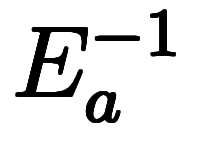




 と分解してから個別に逆演算に直す方が覚えやすく、
と分解してから個別に逆演算に直す方が覚えやすく、




 と両辺の指数変換
と両辺の指数変換 を経ての
を経ての と覚える方が理屈を付けやすいだろう。
と覚える方が理屈を付けやすいだろう。 に対し
に対し と
と しか登場しなければ、
しか登場しなければ、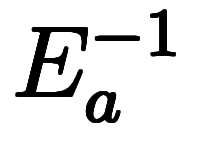 と
と の順番を覚える必要が無くなる。
の順番を覚える必要が無くなる。
小さいことではあるが、片方に付くが他方に付かない「-1」などは、混乱の元でしか無い。