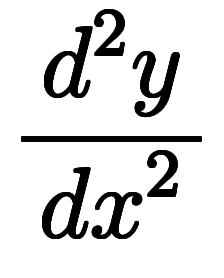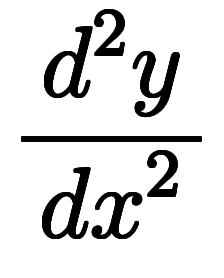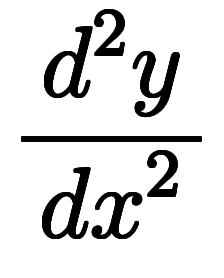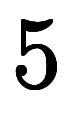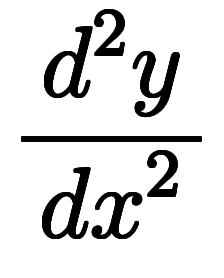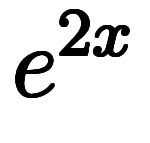![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
定数係数2階線形常微分方程式 のバックアップ(No.1) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
定数係数2階線形常微分方程式 のバックアップ(No.1) |
凌宮読取術: |
| |
⇒ | 線形常微分演算の因数分解 |
⇒ | 2つの1階線形常微分方程式 |



最初の読み替えから演算子部を取り出すと、因数分解した形の式が現れる:
|
読み替えが可能な理由は常微分の線形性によるが、右側の展開で簡単に確認できる。
| |
= |
|
= | |
⇒ |
|
ここで、重要なのは

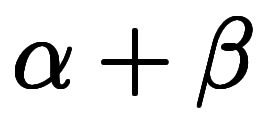 かつ
かつ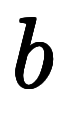


 という関係であり、
という関係であり、
実際 と
と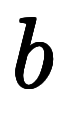 から
から と
と を求めるには、
を求めるには、 についての二次方程式
についての二次方程式



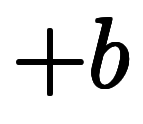

 を解けば良い。
を解けば良い。



因数分解形から連立一階形への変形は、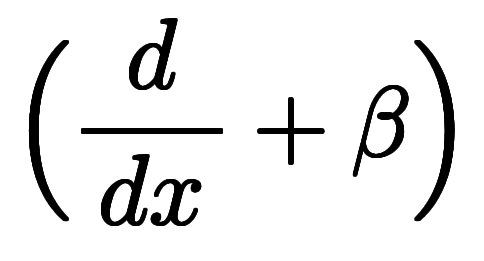
 を
を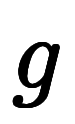 と置いただけである。
と置いただけである。
そうすれば、置き換えられた式も、置く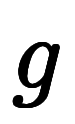 の定義式自体も、自ずと1階線形常微分方程式となる。
の定義式自体も、自ずと1階線形常微分方程式となる。
|
実際、連立も名ばかりのもので、上の式に が無いため、先に
が無いため、先に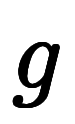 から解けば良い。
から解けば良い。



1階線形常微分の解より、連立した2式の解はそれぞれ次のようになる:
|
|
下式を上式に代入して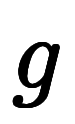 を消せば、解の公式が得られる:
を消せば、解の公式が得られる:
|
この公式を解けば、2つの不定積分で計2つの積分定数が現われて2つの一般解を作る。残りの本体が特殊解となる。
定番の解法に対する最大の特徴は、同次・斉次の場合分けも無ければ、一般解の場合分けも無い点である。
どちらも積分対象の値に応じて積分結果の形が自動的に変わるため、値で場合分けを実現している。
以下に、積和形の公式と定番手法の場合分けの対応例を示す。