![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
定数係数4階線形常微分方程式 のバックアップ(No.7) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
定数係数4階線形常微分方程式 のバックアップ(No.7) |
|
| |
⇔ | 式1: 線形常微分演算子化 |
⇔ | 式2: 線形常微分演算子の因数分解 |
⇔ | 式3: 逆演算子表記 |
⇔ | 式4: 逆演算子を積分に置換*1 |
⇔ | 式5: 4回の逐次積分 |
以下からは具体的な積分計算が始まる。 は全て積分定数。
は全て積分定数。
|
|
|
|
|
|
|
|
|
|


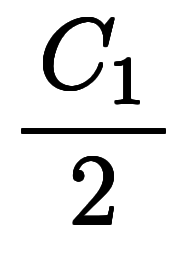 、
、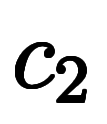

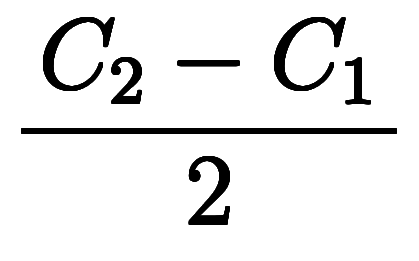 、
、

 、
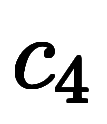
、

 と置けば、複素係数での解集合が得られる。
と置けば、複素係数での解集合が得られる。
|
さらに解集合を実係数に限定したければ、
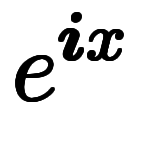


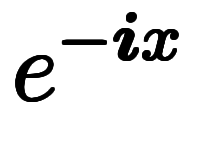 を三角関数で表示してから係数を制限すれば良い。
を三角関数で表示してから係数を制限すれば良い。
改めて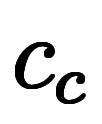



 、
、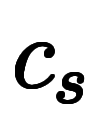

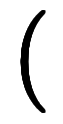



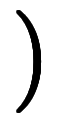
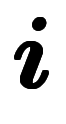 と置いた上で、全ての係数を実数に限定すれば、実数係数での解集合が得られる。
と置いた上で、全ての係数を実数に限定すれば、実数係数での解集合が得られる。
|



|
より、
|
|
|
|