![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
微分積分学の基本公式 のバックアップ(No.24) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
微分積分学の基本公式 のバックアップ(No.24) |
【執筆中】
|
|
歴史的には、別々に発展した微分法と区分求積法という2大分野を繋げた超重要公式である。
現在のベクトル解析では、重要な置換積分公式*1*2*3が全てこの基本公式の拡張版という位置づけ。
問題は、図形と密接に繋がっている基本公式にも関わらず、図による直観的な説明が見掛けない。
微分積分学の基本公式では、微分の結果に対して積分を行うため、
一般的に教えられる「微分は傾き、積分は面積」という考え方では1枚の絵にならない。
体積分は体積、面積分は面積、線積分は線積(?)要は長さを表すのが名前通りの意味。
微分積分の基本公式に出てくる積分は、スカラの線積分であるため、長さを表すように図示できる。
このため、凌宮数学では、基本公式を以下のように読み替え、ベクトル解析の考え方で図示する。
|
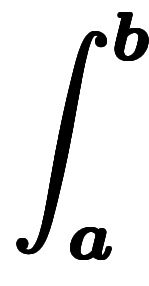
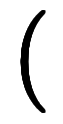

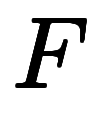
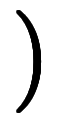


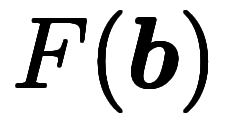

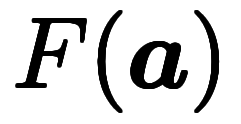 ── 微分積分の基本公式のベクトル版。なぜか慣用名が無い。
── 微分積分の基本公式のベクトル版。なぜか慣用名が無い。
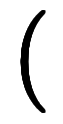
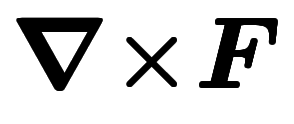


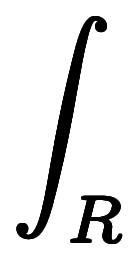


 ── 面積分と線積分を繋ぐ置換積分公式。ストークスの定理。
── 面積分と線積分を繋ぐ置換積分公式。ストークスの定理。
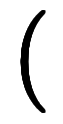



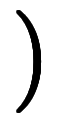





 ── 体積分と面積分を繋ぐ置換積分公式。ガウスの定理。
── 体積分と面積分を繋ぐ置換積分公式。ガウスの定理。





問題を簡単にするため、まず1つの変数 だけについて考える。
だけについて考える。
変数1つしかないから関数を考えなくても良く、関数

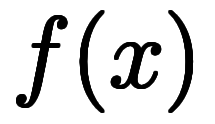 の独立変数と考えても良い。
の独立変数と考えても良い。
とにかく は今、他からの影響を一切受けない、自由な変数である。
は今、他からの影響を一切受けない、自由な変数である。
| File not found: "Δx.png" at page "微分積分学の基本公式"[添付] |
まず、 軸上に2点
軸上に2点 と
と を考える。
を考える。
すると、2点によって区間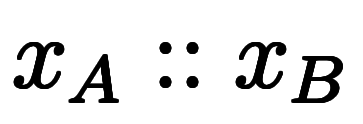 *4が区切られる。
*4が区切られる。
区間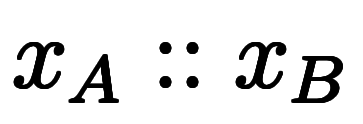 の長さを差分
の長さを差分 と定義すると、
と定義すると、



 と書ける。
と書ける。
| File not found: "δxi.png" at page "微分積分学の基本公式"[添付] |
次に、区間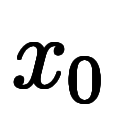
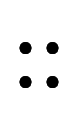
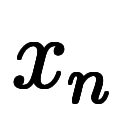 の
の 等分し、分割点を
等分し、分割点を から順に
から順に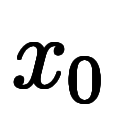 、
、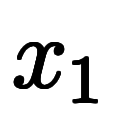 …
…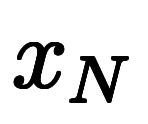 名付けた場合について考える。
名付けた場合について考える。
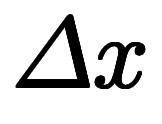 と同様に、区間
と同様に、区間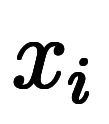
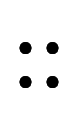
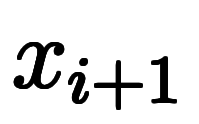 に対応する差分を
に対応する差分を と定義すると、
と定義すると、

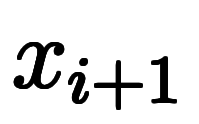

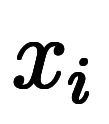 と書ける。
と書ける。
今、区間を単純に分割しているに過ぎないため、 を繋ぎ合わせば必ず
を繋ぎ合わせば必ず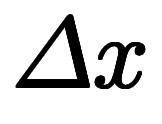 に戻る。
に戻る。
式1: |
| File not found: "dxi.png" at page "微分積分学の基本公式"[添付] |
続けて、分割数 を
を に近づける無限な等分を考える。
に近づける無限な等分を考える。
このとき、 は
は に近づき、
に近づき、 と書かれる微小な量になる。
と書かれる微小な量になる。
式1は分割数 に無関係に成り立つため、無限に分割ても同様の式が成り立つ:
に無関係に成り立つため、無限に分割ても同様の式が成り立つ:
式2: |
ここで、式2の左辺
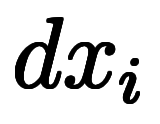 は微小量
は微小量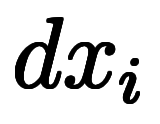 の総和であるため、
の総和であるため、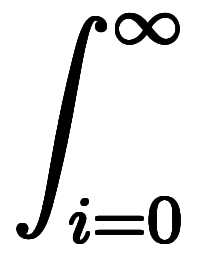
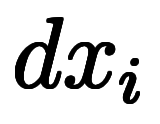 に書き換えられる。
に書き換えられる。
さらに、 のとき
のとき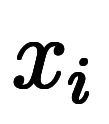

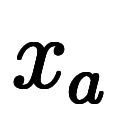 、
、 のとき
のとき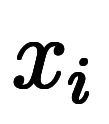

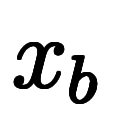 であるため、左辺は
であるため、左辺は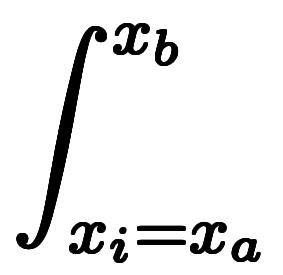
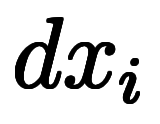 に書き換えられる。
に書き換えられる。
もはや添字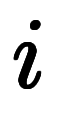 が不要となり、
が不要となり、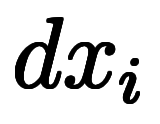 を全て
を全て で代表させて
で代表させて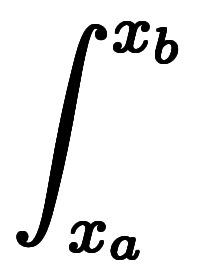
 に書き換えても混乱は起きない。
に書き換えても混乱は起きない。
よって、
式3: |
*5。
区間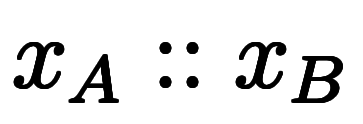 にある全ての
にある全ての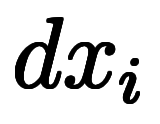 を足し合わせる意味のため、
を足し合わせる意味のため、
微小量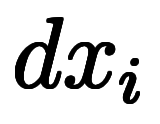 を
を から
から までの積分と同義となる。
までの積分と同義となる。
一応、形式的に次の記号の読み替えで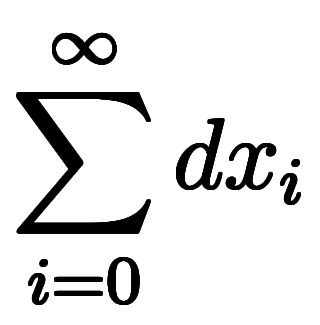

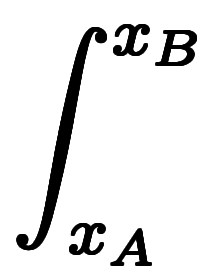
 と考えることができる:
と考えることができる:
| 式2(再掲) |
|
|
| 区間表現では添字が不要になるため、 |
| 微小量を足し合わせるには、 |
|
|
式2において、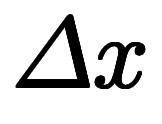 を無限に分割して
を無限に分割して を作る操作が、傾きでない、もう一つの微分であり、
を作る操作が、傾きでない、もう一つの微分であり、
逆に、無数にある を足し合わせて
を足し合わせて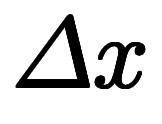 に戻す操作が、面積でない、もう一つの積分である。
に戻す操作が、面積でない、もう一つの積分である。
この微分 は厳密に全微分と呼ばれ、被微分関数を持つ
は厳密に全微分と呼ばれ、被微分関数を持つ のような関数の微分とは異なる概念である。
のような関数の微分とは異なる概念である。
この積分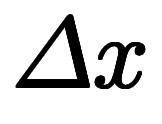 も被積分関数を持たない積分となるが、次の読み替えにより被積分関数が
も被積分関数を持たない積分となるが、次の読み替えにより被積分関数が の関数の積分に含まれる。
の関数の積分に含まれる。
要点を簡潔に纏めると、
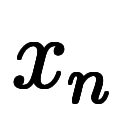 と
と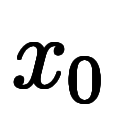 の引き算から、差
の引き算から、差 が得られる。
が得られる。 を分割していくと、差分
を分割していくと、差分 が得られる。
が得られる。 が
が に近づき全微分
に近づき全微分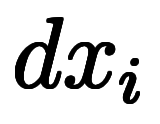 が得られる。
が得られる。File not found: "差.png" at page "微分積分学の基本公式"[添付]







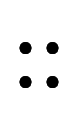
 は閉区間の凌宮表記である。一般的に
は閉区間の凌宮表記である。一般的に![[A,B] $$ [A,B] $$](./eq/eq-ni-4985d76b77bd42b5be03062eed763e2c.png) という表記を用いられるが、紛らわしいため凌宮数学では用いない。
という表記を用いられるが、紛らわしいため凌宮数学では用いない。 の本来の意味で間違いないが、記号としては、区間の一般的な表記法が添字
の本来の意味で間違いないが、記号としては、区間の一般的な表記法が添字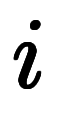 ではなく区間の端点
ではなく区間の端点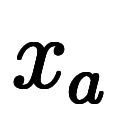 と
と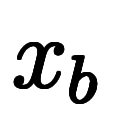 を用いる違いもあることに注意。
を用いる違いもあることに注意。 の本来の意味であるが、標準的な区間の書き方も異なっていることに注意(添字vs両端)。
の本来の意味であるが、標準的な区間の書き方も異なっていることに注意(添字vs両端)。


![\iro[md]{x} $$ \iro[md]{x} $$](./eq/eq-ni-ed85b00cae4c14904b2b4dbe5158adac.png)
![\iro[md]{F} $$ \iro[md]{F} $$](./eq/eq-ni-16b2b770364d08a8286b2ce6fb8adc65.png)
![\iro[md]{0} $$ \iro[md]{0} $$](./eq/eq-ni-e0f0b691cd5e512f0d1f64345ab16f14.png)
![\iro[md]{x_a} $$ \iro[md]{x_a} $$](./eq/eq-ni-8c1d146a11b7c8f4e119822dbaab233f.png)
![\iro[md]{x_b} $$ \iro[md]{x_b} $$](./eq/eq-ni-da6ebf2700ce1376c87b1e3464a9f386.png)
![\iro[md]{F_a} $$ \iro[md]{F_a} $$](./eq/eq-ni-4c2eb32d0ebb72e4dcb026e57e83fef2.png)
![\iro[md]{F_b} $$ \iro[md]{F_b} $$](./eq/eq-ni-78660ef74ba7da558ace81c11996b16c.png)
![\iro[ai]{F} $$ \iro[ai]{F} $$](./eq/eq-ni-167e9b8e6d272d6397304d85327eb57f.png)
![\iro[ai]{x_0} $$ \iro[ai]{x_0} $$](./eq/eq-ni-e5c2956321cb7367384c4c90837074d1.png)
![\iro[ai]{x_1} $$ \iro[ai]{x_1} $$](./eq/eq-ni-8ab850bea4ea138dab483e0d267e54a2.png)
![\iro[ai]{x_2} $$ \iro[ai]{x_2} $$](./eq/eq-ni-0412b85185c68197bd3c0347e19addcf.png)
![\iro[ai]{x_3} $$ \iro[ai]{x_3} $$](./eq/eq-ni-b6aedd6055fe34f68309c35a93485493.png)
![\iro[ai]{x_n} $$ \iro[ai]{x_n} $$](./eq/eq-ni-5a230991110c254acfb43e47e4a6aa86.png)
![\iro[ai]{x_N} $$ \iro[ai]{x_N} $$](./eq/eq-ni-e75ffb88cb538e6f24b2fad2f0bd5a2a.png)
![\iro[ai]{x_\infty} $$ \iro[ai]{x_\infty} $$](./eq/eq-ni-36e6f1ead1a06003fd98bc60a644f5b8.png)
![\iro[ai]{F_0} $$ \iro[ai]{F_0} $$](./eq/eq-ni-3cc6a13b60740f10544be423e6532f4a.png)
![\iro[ai]{F_n} $$ \iro[ai]{F_n} $$](./eq/eq-ni-d90376d10aefab88c1e01ae555ff459f.png)
![\iro[ak]{\gdl F} $$ \iro[ak]{\gdl F} $$](./eq/eq-ni-bf8610a72f3a0a60d0b7322426c10616.png)
![\iro[ak]{\gdl x} $$ \iro[ak]{\gdl x} $$](./eq/eq-ni-e460066873c06acd81b0e35f1bffd7a1.png)
![\iro[ak]{\gdl F_i} $$ \iro[ak]{\gdl F_i} $$](./eq/eq-ni-8870479420a7a2ad04d133b755067006.png)
![\iro[ak]{\gdl x_i} $$ \iro[ak]{\gdl x_i} $$](./eq/eq-ni-a58ef858d91b3d8982cd501d9b57651c.png)
![\iro[ai]{x_i} $$ \iro[ai]{x_i} $$](./eq/eq-ni-6f10db103a8aa52fb4a24478b9cdf918.png)
![\iro[ai]{x_{i+1}} $$ \iro[ai]{x_{i+1}} $$](./eq/eq-ni-7705d5906dbaaf8aaaef2cf35a35918d.png)
![\iro[ai]{F_i} $$ \iro[ai]{F_i} $$](./eq/eq-ni-fbfe24bb5e3e280de317864cb8a094e3.png)
![\iro[ai]{F_{i+1}} $$ \iro[ai]{F_{i+1}} $$](./eq/eq-ni-4e5157ad5e50abbf7e4ad63a12756d69.png)
![\iro[ak]{\gdl x_0} $$ \iro[ak]{\gdl x_0} $$](./eq/eq-ni-9e558102f4f540a9db3f9460f6e5f405.png)
![\iro[ak]{\gdl F_0} $$ \iro[ak]{\gdl F_0} $$](./eq/eq-ni-f1071aa588d0f9a83b109fd3976a4988.png)
![\iro[ak]{\gdl x_1} $$ \iro[ak]{\gdl x_1} $$](./eq/eq-ni-462953258e683427e6ee0c6f299ba065.png)
![\iro[ak]{\gdl F_1} $$ \iro[ak]{\gdl F_1} $$](./eq/eq-ni-5b3b147881c7ad99c1b39b619d5b4ad2.png)
![\iro[ak]{\gdl x_i} $$ \iro[ak]{\gdl x_i} $$](./eq/eq-ni-a58ef858d91b3d8982cd501d9b57651c.png)
![\iro[ak]{\gdl F_i} $$ \iro[ak]{\gdl F_i} $$](./eq/eq-ni-8870479420a7a2ad04d133b755067006.png)
![\iro[ak]{\gdl x_N} $$ \iro[ak]{\gdl x_N} $$](./eq/eq-ni-c4445bd4482a75e80011074e5db5c649.png)
![\iro[ak]{\gdl F_N} $$ \iro[ak]{\gdl F_N} $$](./eq/eq-ni-3dfff019eac8f7df6a9f4d2710a11a8c.png)
![\iro[ak]{\gdl x_\infty} $$ \iro[ak]{\gdl x_\infty} $$](./eq/eq-ni-7efc20e63a68fe5e5349c21ceaf2e173.png)
![\iro[ak]{\gdl F_\infty} $$ \iro[ak]{\gdl F_\infty} $$](./eq/eq-ni-e22049634087d0ab1cf66086df4f971c.png)
![\iro[ai]{\cdots} $$ \iro[ai]{\cdots} $$](./eq/eq-ni-6a31a92685217938ec7249d4821d2a05.png)
![\iro[ak]{\cdots} $$ \iro[ak]{\cdots} $$](./eq/eq-ni-54d1d6382e27c0af6692cfd766b4939d.png)
![\iro[ak]{dF} $$ \iro[ak]{dF} $$](./eq/eq-ni-255a7309c685470b053702bba75678fb.png)
![\iro[ak]{dx} $$ \iro[ak]{dx} $$](./eq/eq-ni-5f320f63a3fd21c36ab168c2cb9dd555.png)