![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
微分積分学の基本公式 |
凌宮読取術: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
これは、歴史的に別々に発展した微分法と区分求積法を繋げた超重要定理の一部*1である。
また、現在のベクトル解析においては、重要な置換積分公式*2*3*4が全てこの公式の拡張と言える。
問題は、図形と密接に繋がっている公式にも関わらず、図による直観的な説明は見掛けない。
微分積分学の基本公式では、微分の結果に対して積分を行うため、
一般的に教えられる「微分は傾き、積分は面積」という考え方では両立せず、1枚の絵に纏まらない。
これに対し、凌宮数学では、線積分に基づき、積分の解釈を面積ではなく線長とし、
微分積分の基本公式を1枚の図に纏めて、微積関係を直観的に読み取る:
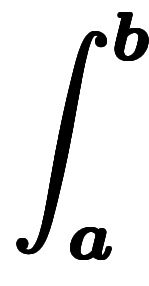
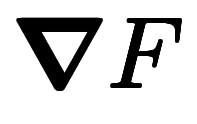



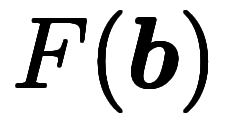

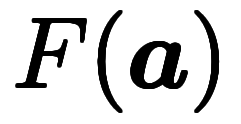 ── 微分積分の基本公式のベクトル版。なぜか慣用名は無い。
── 微分積分の基本公式のベクトル版。なぜか慣用名は無い。
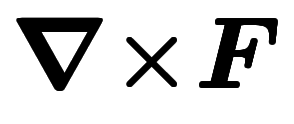
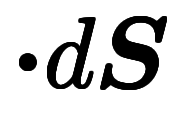

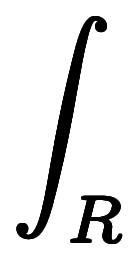


 ── 面積分と線積分を繋ぐ置換積分公式。ストークスの定理。
── 面積分と線積分を繋ぐ置換積分公式。ストークスの定理。








 ── 体積分と面積分を繋ぐ置換積分公式。ガウスの定理。
── 体積分と面積分を繋ぐ置換積分公式。ガウスの定理。





第1段階では、問題を簡単にするべく、1つの変数 から始める。
から始める。
今の は、他からの影響を一切受けない、自由な変数である。
は、他からの影響を一切受けない、自由な変数である。
まずは、 軸と軸上に2点
軸と軸上に2点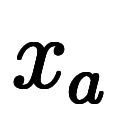 と
と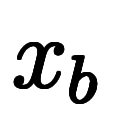 がある場合を考える。
がある場合を考える。
2点によって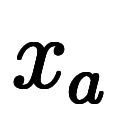



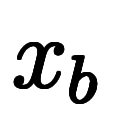 になる区間
になる区間 *5が区切られる。
*5が区切られる。
区間 の長さは、2点の差
の長さは、2点の差

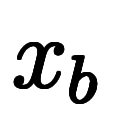

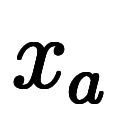 で与えられる。
で与えられる。
つぎに、区間 を
を 分割して、分割点を
分割して、分割点を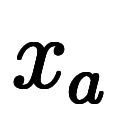 から順に
から順に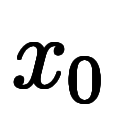 、
、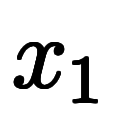 …
…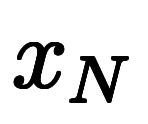 と名付ける。
と名付ける。
小さくなるが、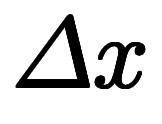 と同様に、区間
と同様に、区間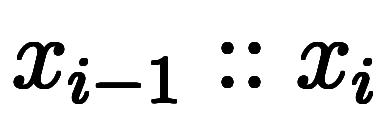 の長さは端点の差分
の長さは端点の差分

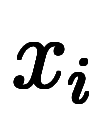

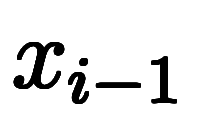 で与えられる*6。
で与えられる*6。
差分と呼ぶが、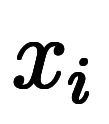 が数列っぽく、
が数列っぽく、 が小さいというだけで、差
が小さいというだけで、差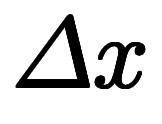 とは本質的に何も変わらない。
とは本質的に何も変わらない。
ポイントは、区間を単純に分割しているため、 を繋ぎ合わせば必ず
を繋ぎ合わせば必ず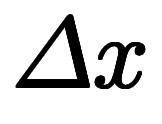 に戻るという関係。
に戻るという関係。
式1: |
続けて、分割数 を無限に増やしてみる。
を無限に増やしてみる。
 が
が に近づくため、
に近づくため、 は
は に近づく。
に近づく。
この に近い微小量という意味を込めて
に近い微小量という意味を込めて を
を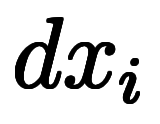 と表記し、
と表記し、 の微分*7と呼ぶ。
の微分*7と呼ぶ。
一方で、式1は分割数 に無関係に成り立つため、無限に分割ても同様の式が成り立つ:
に無関係に成り立つため、無限に分割ても同様の式が成り立つ:
式2: |
最後に、左辺の
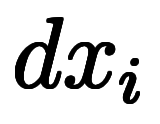 は微小量
は微小量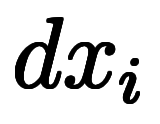 の総和であるため、
の総和であるため、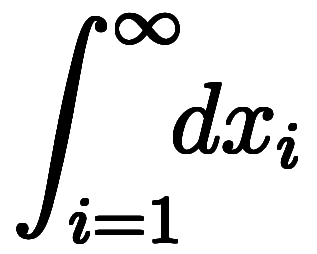 に書き換えできる*8
に書き換えできる*8
今は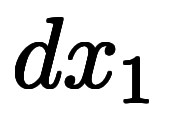 の下端が
の下端が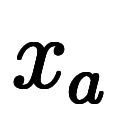 、
、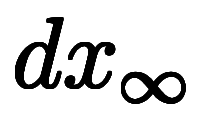 の上端が
の上端が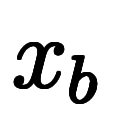 であるため、
であるため、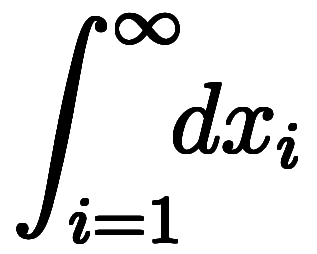

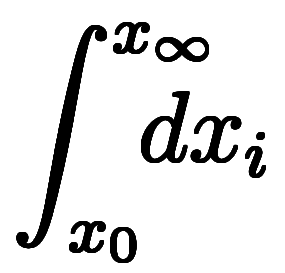

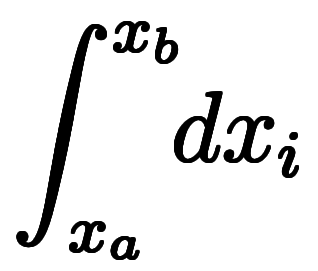 は全て同じ意味である。
は全て同じ意味である。
区間の端点で表せたため、範囲の指定に使っていた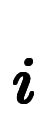 は今や不要となる*9:
は今や不要となる*9:
式3: |
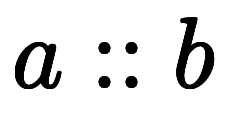 は凌宮数学の閉区間表記である。
は凌宮数学の閉区間表記である。![[a,b] $$ [a,b] $$](./eq/eq-ni-ca400ab3f30b1ab90106538b85afbd2e.png) で表記されるが、優先順位の括弧と紛らわしいため凌宮数学では用いない。
で表記されるが、優先順位の括弧と紛らわしいため凌宮数学では用いない。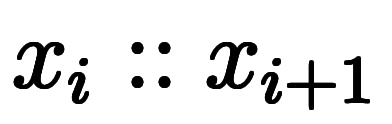 を
を と対応させるように、下端の添字を揃える場合が多い。
と対応させるように、下端の添字を揃える場合が多い。

 や
や

 になる煩雑を避けるため、上端に揃えた。そのため、総和の下端は1から始る。
になる煩雑を避けるため、上端に揃えた。そのため、総和の下端は1から始る。 のような一般的な微分とは全く別物である。区別のため「全微分」で呼ばれる場合がある。
のような一般的な微分とは全く別物である。区別のため「全微分」で呼ばれる場合がある。 の本来の意味である。
の本来の意味である。 と書くだけで、各点における
と書くだけで、各点における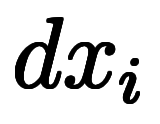 の意味合いを持つ。
の意味合いを持つ。


第2段階として、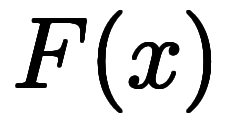 を想定した、従属変数
を想定した、従属変数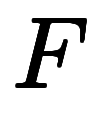 を考える。
を考える。
従属変数も変数である以上、独立変数 と同じように考えられる。
と同じように考えられる。
以下は、従属変数らしく縦軸で描くが、 の纏めも兼ねて要点に絞る。
の纏めも兼ねて要点に絞る。
まずは、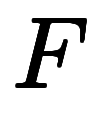 軸と2点
軸と2点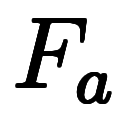 、
、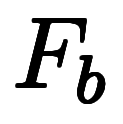 があれば、長さ
があれば、長さ の区間
の区間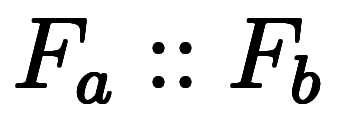 が1つ区切られる。
が1つ区切られる。
つぎに、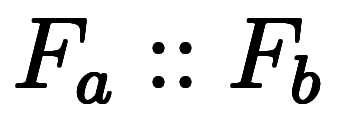 を分割すれば、長さ
を分割すれば、長さ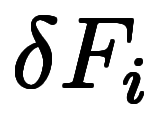 の区間が大量に作られ、繋げば
の区間が大量に作られ、繋げば に戻る。
に戻る。
式4: |
続けて、無限に分割すれば、長さ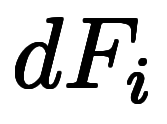 の区間が無限に作られ、繋げばやはり
の区間が無限に作られ、繋げばやはり に戻る。
に戻る。
式5: |
最後に、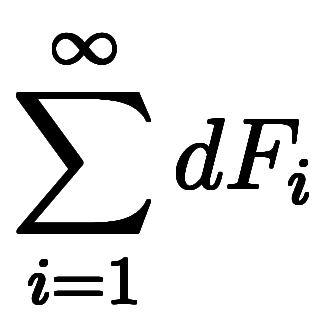

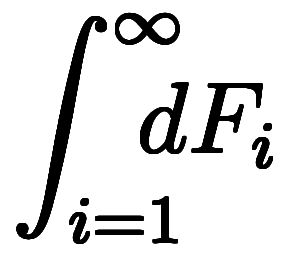

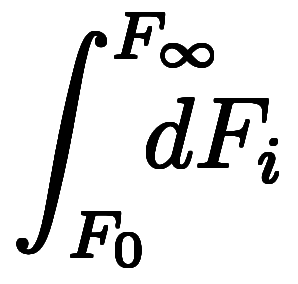

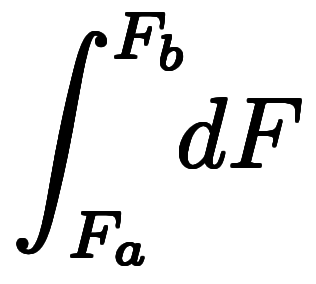 は、全て同じ意味であり、積分らしく〆て:
は、全て同じ意味であり、積分らしく〆て:
式6: |
纏めると、 や
や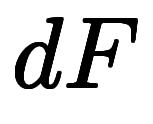 などの全微分は区間の無限分割、対する積分は微小区間の足し合わせ。
などの全微分は区間の無限分割、対する積分は微小区間の足し合わせ。
微分積分学の基本公式の1つ目の読み方は:
|



第3段階として、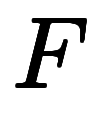 と
と の関係を考える。
の関係を考える。
ここに来て初めて2つの変数が出揃うので、横軸 、縦軸
、縦軸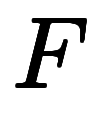 の見慣れた2次元グラフが登場する。
の見慣れた2次元グラフが登場する。
手口はこれまで同様、2点の場合、適当に分割した場合、無限に分割した場合を順に進める。
まずは、 軸と2点
軸と2点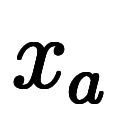 と
と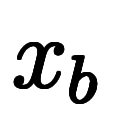 、直交する
、直交する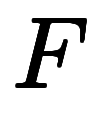 軸と2点
軸と2点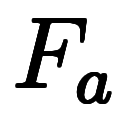

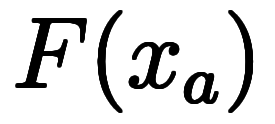 、
、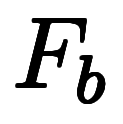

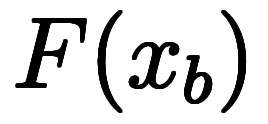 について考える。
について考える。
軸上に2点があれば、長さ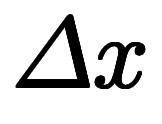 の区間
の区間 と長さ
と長さ の区間
の区間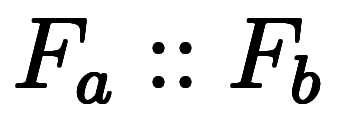 が区切られる。
が区切られる。
2つの差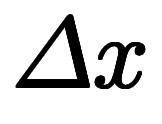 と
と の関係を無理やり式で表すと*10*11*12:
の関係を無理やり式で表すと*10*11*12:
式7: |
つぎに、 を分割し、
を分割し、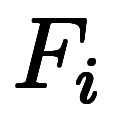

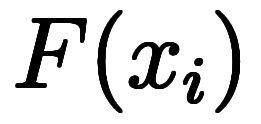 の関係を保ちながら
の関係を保ちながら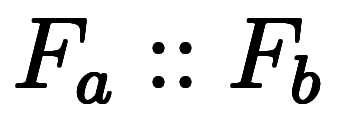 も分割する。
も分割する。
対応する2つの差分 と
と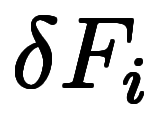 に着目すると、式7の差と全く同じ関係が成り立つ:
に着目すると、式7の差と全く同じ関係が成り立つ:
式8: |
続けて、 を無限に分割する。
を無限に分割する。
 と
と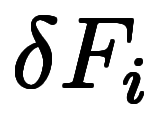 が小さくなるだけで何も変わらないため、式8の差分と全く同じ関係が成り立つ:
が小さくなるだけで何も変わらないため、式8の差分と全く同じ関係が成り立つ:
式9: |
最後に、対応していることが分かれば良いので、添字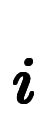 を省けば:
を省けば:
式10: |
纏めると、 や
や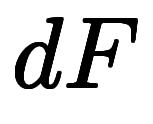 などの全微分の乗算と除算は差分量に同じ。微分積分学の基本公式の2つ目の読み方は:
などの全微分の乗算と除算は差分量に同じ。微分積分学の基本公式の2つ目の読み方は:
|


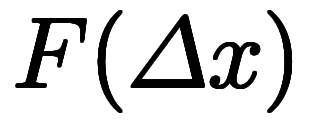 であることに注意。
であることに注意。 も
も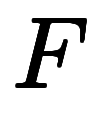 の関係も具体的に分からない場合、
の関係も具体的に分からない場合、

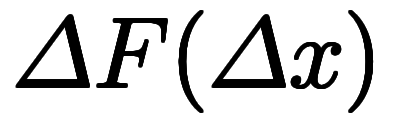 と関数記号で書くは王道だが、強引に恒等式で書く手法もある。
と関数記号で書くは王道だが、強引に恒等式で書く手法もある。



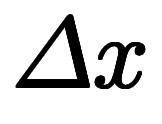

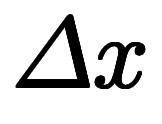 など色々作れて、除算と乗算を選ぶ理由は特に無いが、除算と乗算を選べば微分と積分に繋がる。
など色々作れて、除算と乗算を選ぶ理由は特に無いが、除算と乗算を選べば微分と積分に繋がる。


これまで、「差 」→「差分
」→「差分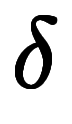 」→「微分
」→「微分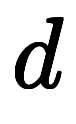 」と区間を小さくする手順を繰り返してきた。
」と区間を小さくする手順を繰り返してきた。
それぞれで得た式を並べば、区間を小さくしただけで、他は何も変わらないことは直観で分かる。
| 差と和 | 商と積 | 微分・積分の基本公式 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 差 | ![\iro[hi]{\sum} $$ \iro[hi]{\sum} $$](./eq/eq-ni-58162b87279200f5ec7e5942b5621766.png)  |  |  |  |  | 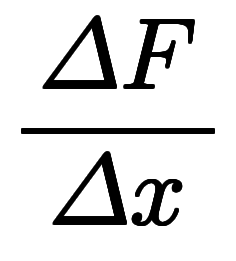 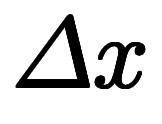 | ![\iro[hi]{\sum} $$ \iro[hi]{\sum} $$](./eq/eq-ni-58162b87279200f5ec7e5942b5621766.png) 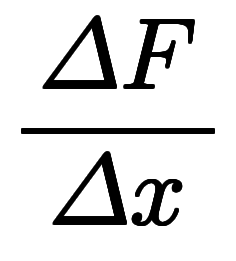 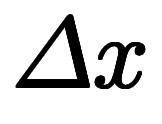 |  | ![\iro[hi]{\sum} $$ \iro[hi]{\sum} $$](./eq/eq-ni-58162b87279200f5ec7e5942b5621766.png)  |  |  |
| 差分 |  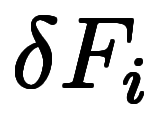 |  |  | 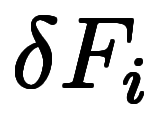 |  |   |   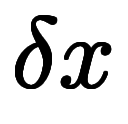 |  |  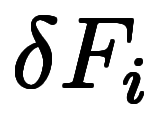 |  |  |
| 微分 |  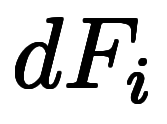 |  |  | 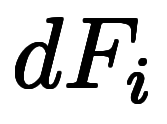 |  |  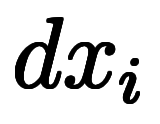 |   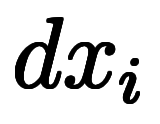 |  |  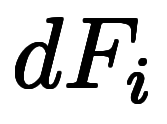 |  |  |
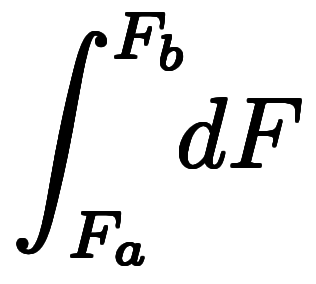 |  |  | 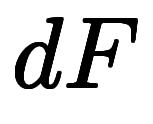 |  |   | 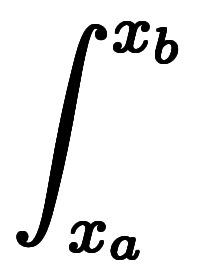   |  | 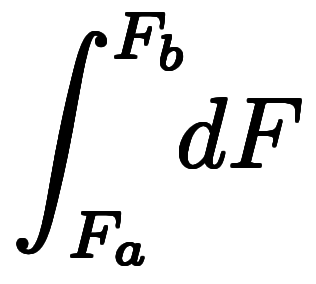 |  |  | |
また、微分積分学の基本公式の一般的な説明では「近似誤差」と「極限で に収束する概念」が必須である*13*14が、
に収束する概念」が必須である*13*14が、
上記の区間を狭める各過程において、差と和、商と積の式は常に厳密に一致していることに注意する必要がある。
これは差分商を上手く設定しているためで、通常の説明で用いられる微分ありきの差分商とは条件が異なっている。



これまで、微分積分の基本公式を直観的に理解するため、全微分と全積分に基づく一連の図を描いた。
これらの図では、差→差分→微分と変化させながら、基本公式を不変の関係として直観的に捉えられる。
微分積分の基本公式は、ベクトル解析の分野で大きな影響力を持っている。
この考え方は、線積分、面積分、体積分の間にある置換積分公式の図による直観的理解に繋ぐ。



微分積分の直観的理解のため、変数の微分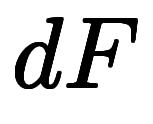 とその積分
とその積分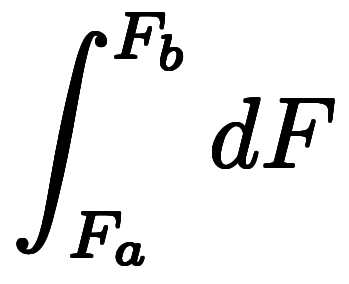 について考えた。
について考えた。
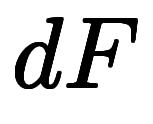 は全微分とも呼ばれ、偏微分など*15と呼ばれる微分とは異なる*16*17*18*19。
は全微分とも呼ばれ、偏微分など*15と呼ばれる微分とは異なる*16*17*18*19。
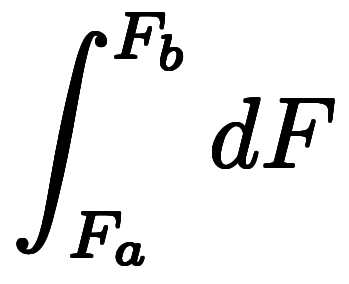 は被積分関数が
は被積分関数が の積分として括られるが、凌宮数学では微分に対応させ全積分と呼び分ける。
の積分として括られるが、凌宮数学では微分に対応させ全積分と呼び分ける。
| 系統名(仮案) | 全微分 | 偏微分 | 全積分 | 偏積分 | |
|---|---|---|---|---|---|
| 変数の微分 | 関数の微分 | 変数の積分 | 関数の積分 | ||
| 慣用名 | 略称 | 微分 | 微分 | 積分 | |
| 1変数 | 全微分 | 常微分 | 定積分 | ||
| 多変数 | 偏微分 | 線積分 | |||
| 表記例 | 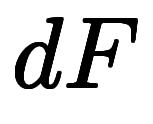 、 、 |  | 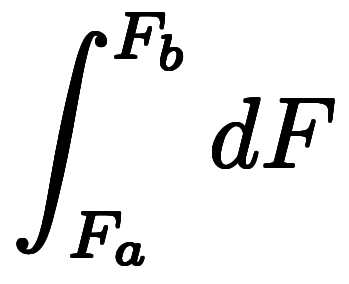 、 、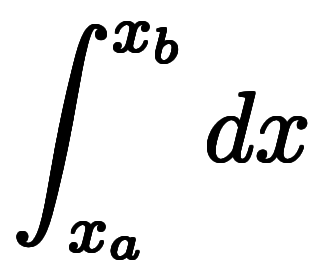 | 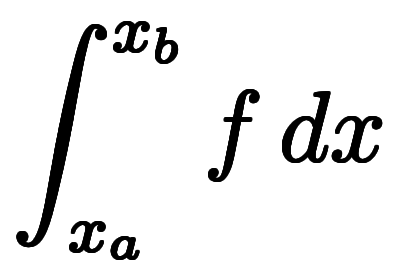 | |
全微分は特定の変数だけの微小量であり、全積分はその逆演算として、微小量の総和である差を表す。
偏微分は関数と変数の関係であり、偏積分はその逆演算として、やはり関数と変数の関係を表す。
また、偏微分は2つの全微分の商とも見なせて、この解釈では偏積分は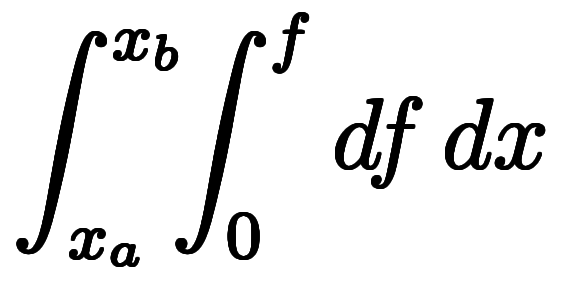 として2つの全微分の積と見なせる。
として2つの全微分の積と見なせる。
微分積分の基本公式



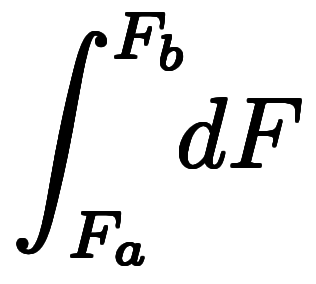

 では、
では、


 が導関数
が導関数 と変数
と変数 の偏積分、
の偏積分、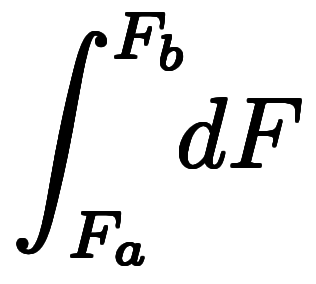 が変数
が変数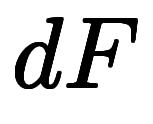 の全積分と見なせるため、
の全積分と見なせるため、
微分積分の基本公式は偏積分と全積分を結ぶ変換公式であるとも言える。
※ 日本語の「微分」も「全微分」も複数の概念を表している*20。
英語でも多少の揺れはあるが、![\iro[ak]{dF} $$ \iro[ak]{dF} $$](./eq/eq-ni-255a7309c685470b053702bba75678fb.png) の形の微分を「differential」と、
の形の微分を「differential」と、![\iro[ak]{\ddd{F}{x}} $$ \iro[ak]{\ddd{F}{x}} $$](./eq/eq-ni-8d2acc855c3a5f330e465346285d3cfd.png) の形の微分を「derivative」と呼び分けている*21*22*23。
の形の微分を「derivative」と呼び分けている*21*22*23。
漢字を使う中国語でも結構の揺れはあるが、![\iro[ak]{dF} $$ \iro[ak]{dF} $$](./eq/eq-ni-255a7309c685470b053702bba75678fb.png) の形の微分を「微分」と、
の形の微分を「微分」と、![\iro[ak]{\ddd{F}{x}} $$ \iro[ak]{\ddd{F}{x}} $$](./eq/eq-ni-8d2acc855c3a5f330e465346285d3cfd.png) の形の微分を「導数」と呼び分けている。
の形の微分を「導数」と呼び分けている。
現時点で「全微分」と「偏微分」で微分・積分対象の有無の違いを表すのは不適切と認識している*24*25。
【追記】「全導関数」の用例*26が見つかった。「全導関数・偏導関数」vs「全微分・偏微分」の使い分けが既に存在するなら、そのまま使うのもアリかと。その場合、積分の方は「全原関数・偏原関数」vs「全積分・偏積分」と呼べば対応関係を表せる。



全微分自体をベクトルとして扱う視点で、微分の用語をベクトルの用語と照らし合わせて分類すると以下の表になる。
ここで、具体例は以下の場合について考える:
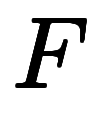

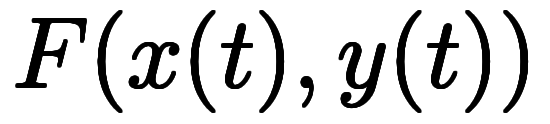 の微分
の微分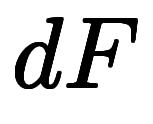









 の成分分解
の成分分解

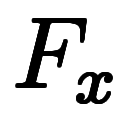
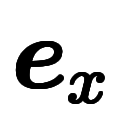

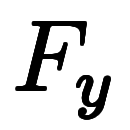


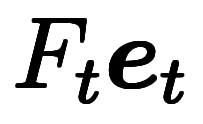
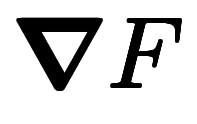 と方向微分係数
と方向微分係数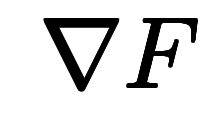

 を示す。
を示す。| 微分 | ベクトル | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 具体例 | 用語 | 具体例 | 用語 | |||||||||
 | 全微分 | 完全微分 | 微分 |  | ベクトル | ベクトル | ||||||
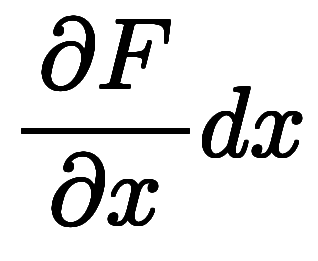 | 不完全微分 | 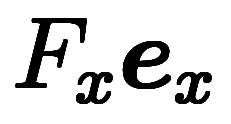 | 成分 | ベクトル成分 | ||||||||
 | 偏微分 | 偏導関数 | 偏微分係数 | 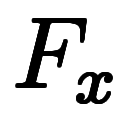 | スカラ成分 成分 | スカラ | ||||||
 | 微分 | 常微分 | 微分商 | 導関数 | 全導関数 | 微分係数 | 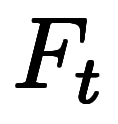 | |||||
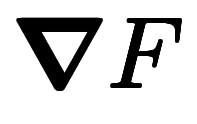 | 勾配 | 全導関数 | 全微分係数 | |||||||||
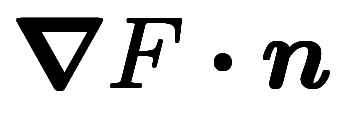 | 方向導関数 | 方向微分係数 | ||||||||||