![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
微分積分学の基本公式 のバックアップ(No.32) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
微分積分学の基本公式 のバックアップ(No.32) |
【執筆中】
|
|
歴史的には、別々に発展した微分法と区分求積法という2大分野を繋げた超重要公式である。
現在のベクトル解析では、重要な置換積分公式*1*2*3が全てこの基本公式の拡張版に相当する。
問題は、図形と密接に繋がっている基本公式にも関わらず、図による直観的な説明が見掛けない。
微分積分学の基本公式では、微分の結果に対して積分を行うため、
一般的に教えられる「微分は傾き、積分は面積」という考え方では1枚の絵にならない。
体積分は体積、面積分は面積、線積分は線積(?)要は長さを表すのが名前通りの意味。
微分積分の基本公式に出てくる積分は、スカラの線積分であるため、長さを表すように図示できる。
このため、凌宮数学では、基本公式を以下のように読み替え、ベクトル解析の考え方で図示する。
|
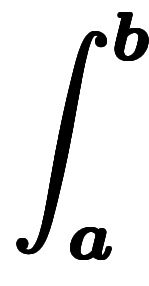
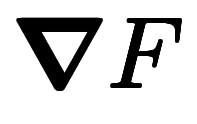



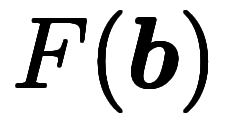

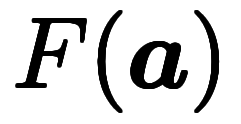 ── 微分積分の基本公式のベクトル版。なぜか慣用名は無い。
── 微分積分の基本公式のベクトル版。なぜか慣用名は無い。
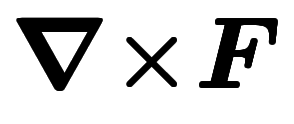
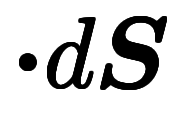

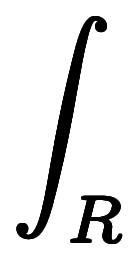


 ── 面積分と線積分を繋ぐ置換積分公式。ストークスの定理。
── 面積分と線積分を繋ぐ置換積分公式。ストークスの定理。








 ── 体積分と面積分を繋ぐ置換積分公式。ガウスの定理。
── 体積分と面積分を繋ぐ置換積分公式。ガウスの定理。





第1段階として、問題を簡単にするべく1つの変数 から始める。
から始める。
1つの変数しか考えないので、関数は考えなくて良い*4。
今の は、他からの影響を一切受けない、自由な変数である。
は、他からの影響を一切受けない、自由な変数である。
まずは、 軸と軸上に2点
軸と軸上に2点 と
と があるとする。
があるとする。
2点によって区間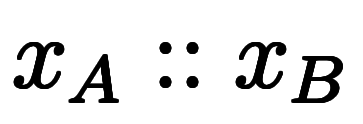 *5が区切られる。
*5が区切られる。
区間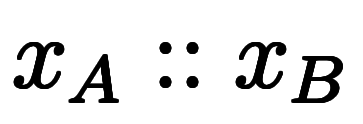 の長さは、2点の差分
の長さは、2点の差分



 で与えられる。
で与えられる。
つぎに、区間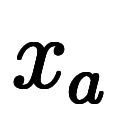
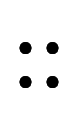
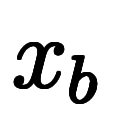 を
を 分割して、分割点を
分割して、分割点を から順に
から順に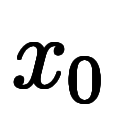 、
、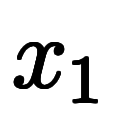 …
…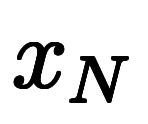 と名付ける。
と名付ける。
小さくなるが、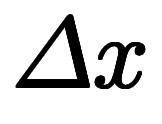 と同様に、区間
と同様に、区間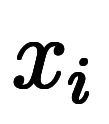
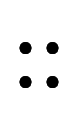
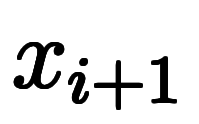 の長さは端点の差分
の長さは端点の差分

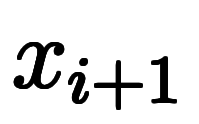

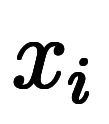 で与えられる。
で与えられる。
また、今は区間を単純に分割しているため、 を繋ぎ合わせば必ず
を繋ぎ合わせば必ず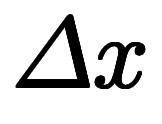 に戻る。
に戻る。
式1: |
続けて、分割数 を無限に増やしてみる。
を無限に増やしてみる。
 が
が に近づくため、
に近づくため、 は
は に近づく。
に近づく。
この に近い微小量という意味を込めて
に近い微小量という意味を込めて を
を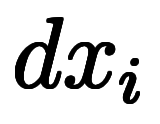 と置く。
と置く。
一方で、式1は分割数 に無関係に成り立つため、無限に分割ても同様の式が成り立つ:
に無関係に成り立つため、無限に分割ても同様の式が成り立つ:
式2: |
式2の左辺
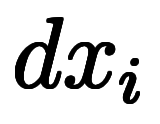 は微小量
は微小量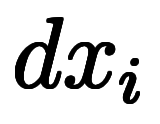 の総和であるため、
の総和であるため、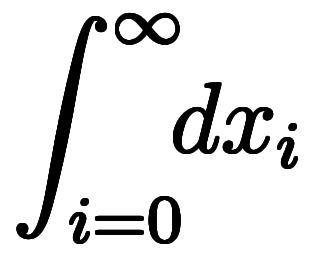 に書き換えできる*6
に書き換えできる*6
今は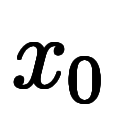

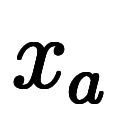 、
、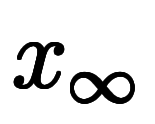

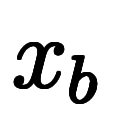 であるため、左辺は
であるため、左辺は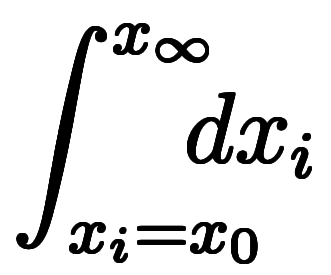

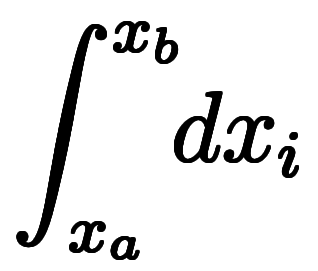 に書き換えできる。
に書き換えできる。
区間の短点で範囲を表せたので、範囲の指定に使っていた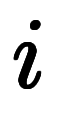 は不要になる:
は不要になる:
式3: |
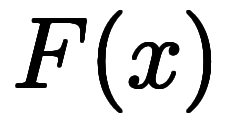 が頭から離れられないなら、その独立変数
が頭から離れられないなら、その独立変数 と考えても良い。
と考えても良い。
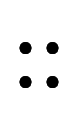
 は凌宮数学の閉区間表記である。一般的に閉区間は括弧表記
は凌宮数学の閉区間表記である。一般的に閉区間は括弧表記![[A,B] $$ [A,B] $$](./eq/eq-ni-4985d76b77bd42b5be03062eed763e2c.png) で表記されるが、優先順位の括弧と紛らわしいため凌宮数学では用いない。
で表記されるが、優先順位の括弧と紛らわしいため凌宮数学では用いない。 の本来の意味である。
の本来の意味である。


第2段階として、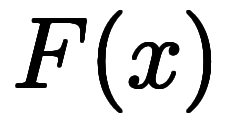 を想定した、従属変数
を想定した、従属変数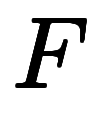 を考える。
を考える。
従属変数も変数である以上、独立変数 と同じように考えられる。
と同じように考えられる。
以下は、従属変数らしく(?)縦軸で描くが、 の纏めも兼ねて要点に絞る。
の纏めも兼ねて要点に絞る。
| File not found: "Fの微差分.png" at page "微分積分学の基本公式"[添付] |
まずは、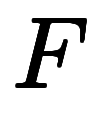 軸と2点
軸と2点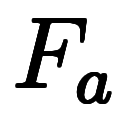 、
、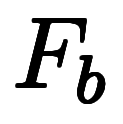 があり、長さ
があり、長さ の区間
の区間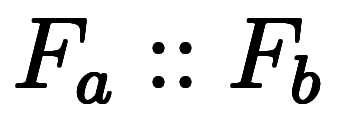 が区切られる。
が区切られる。
つぎに、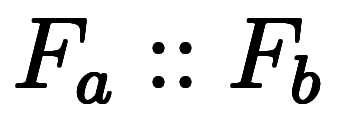 を分割すれば、長さ
を分割すれば、長さ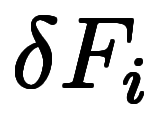 の区間が大量に作られ、繋げば
の区間が大量に作られ、繋げば
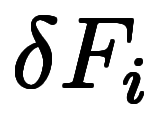

 に戻る。
に戻る。
続けて、無限に分割すれば、長さ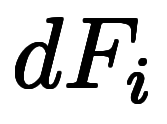 の区間が無限に作られ、繋げばやはり
の区間が無限に作られ、繋げばやはり
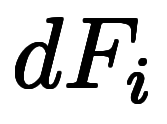

 に戻る。
に戻る。
最後に、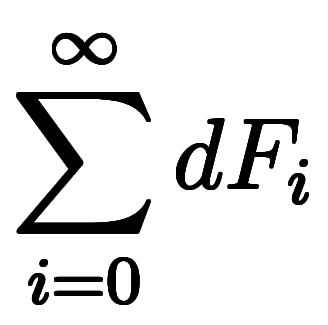 、
、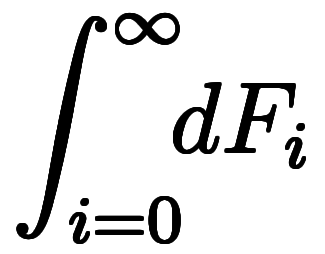 、
、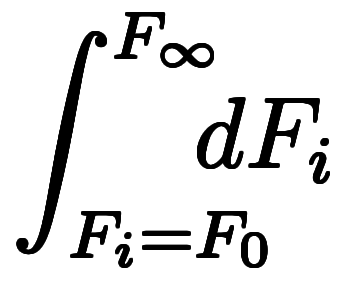 、
、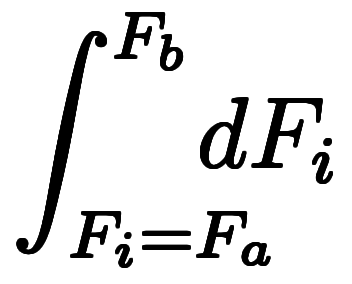 、
、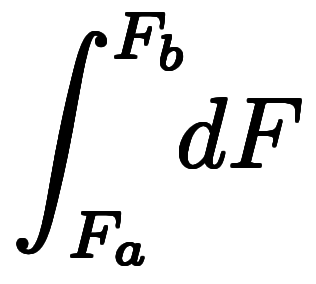 は、全て同じ意味であり、積分らしく〆て:
は、全て同じ意味であり、積分らしく〆て:
式4: |



第3段階として、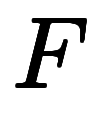 と
と の関係を考える。
の関係を考える。
ここに来て初めて2つの変数が出揃うので、横軸 、縦軸
、縦軸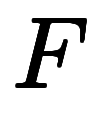 の見慣れた2次元グラフが登場する。
の見慣れた2次元グラフが登場する。
手口はこれまで同様、2点の場合、適当に分割した場合、無限に分割した場合を順に進める。
| File not found: "差商.png" at page "微分積分学の基本公式"[添付] | File not found: "差分商.png" at page "微分積分学の基本公式"[添付] | File not found: "微分商.png" at page "微分積分学の基本公式"[添付] |
まずは、直交する 軸と
軸と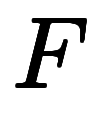 軸、そして、
軸、そして、 軸上の2点
軸上の2点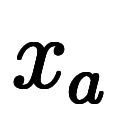 と
と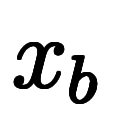 、対応する
、対応する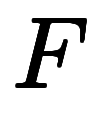 軸上の
軸上の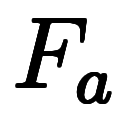 と
と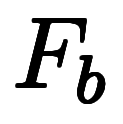 について考える。
について考える。
各軸に区切られる区間は、長さ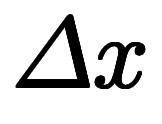 の
の と長さ
と長さ の
の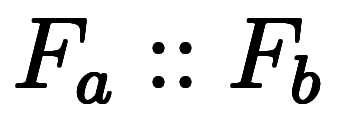 。
。
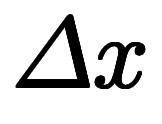 と
と の関係を無理やり式で表すと*7*8:
の関係を無理やり式で表すと*7*8:
式5: |
つぎに、 を分割し、
を分割し、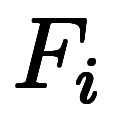

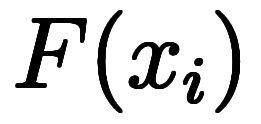 の関係を保ちながら
の関係を保ちながら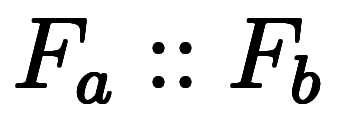 も分割する。
も分割する。
続けて、無限に分割する。





