![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
変換行列の連鎖則 のバックアップ(No.2) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
変換行列の連鎖則 のバックアップ(No.2) |
背景 |
|
|
以下では、この因数分解の幾何的意味を考える。






一般に、2次元の極座標系は![\left\{\arr[l]{ x = r\cos\phi \\ y = r\sin\phi \\ }\right. $$ \left\{\arr[l]{ x = r\cos\phi \\ y = r\sin\phi \\ }\right. $$](./eq/eq-ni-3b9ea3db4a9a65523a612ebdd000b8ae.png) で定義され*1、
で定義され*1、
変換行列は以下のように表せる:
|
変換行列の行列式であるヤコビアンを計算すると:
|
よって、置換積分は


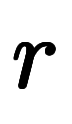

 と書ける。
と書ける。
これは、 と
と 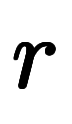
 の積と見なせて、
の積と見なせて、
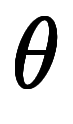 が無次元のため、計量
が無次元のため、計量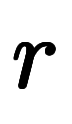 で長さの次元を帳尻合わせしていると解釈できる。
で長さの次元を帳尻合わせしていると解釈できる。
ここで、変換行列から計量を分離すると、回転行列が残った式が得られる:
|



3次元極座標系に対しても同様に考察すると、
ヤコビアンを頑張って計算すれば、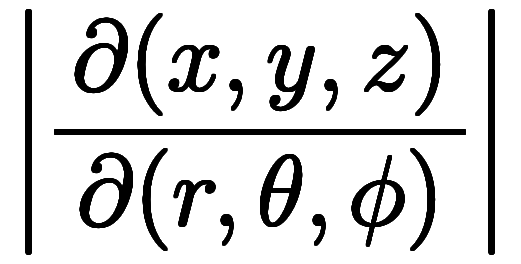

 を得られて、
を得られて、
置換積分は






 と書ける。
と書ける。
類推から と
と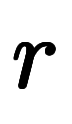
 と
と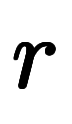

 の積と見なせて、
の積と見なせて、
各次元の帳尻合わせと解釈できる。
特に 方向の計量は、
方向の計量は、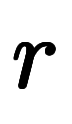 に依存するのみならず
に依存するのみならず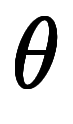 にも依存するのが、
にも依存するのが、
同じ半径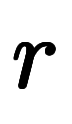 の球面上における異なる
の球面上における異なる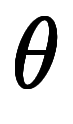 の円周が異なるためと解釈できる。
の円周が異なるためと解釈できる。