基底による常微分と偏微分の区別のバックアップ(No.9)

概要

一般に、微分には常微分と偏微分の区別がある。
関数 $$ f $$ $$ = $$ $$ f(x,t) $$ で、かつ、 $$ x $$ $$ = $$ $$ x(t) $$ のとき、
$\ddd{f}{t}$ $$ = $$ $\ppd{f}{x}$ $\ddd{x}{t}$ $$ + $$ $\ppd{f}{t}$ の形で常微分 $\ddd{f}{t}$ と偏微分 $\ppd{f}{t}$ が同時に登場する。

他方、凌宮数学では逆基底を導入し、全微分をベクトルの成分分解に帰着させている。
その結果、偏微分も全微分も同一の $$ d $$ で表記すべき、という結果が得られた。
しかし、 $\ddd{f}{t}$ $$ = $$ $\ppd{f}{x}$ $\ddd{x}{t}$ $$ + $$ $\ppd{f}{t}$ の $\partial$ と $$ d $$ を統一しては常微分と偏微分の混同が生じる。

以下、逆基底の観点から常微分と偏微分の表記法を再考する。

逆基底による微分の意味付け

微分と座標系の関係

凌宮数学では双対基底に基づき逆基底を導入している。
ベクトル除算が唯一の解に決まらないのに対し、逆基底は唯一に決まる。
そのため、逆基底にはベクトルよりも座標系という情報が多く含まれている。

例えば、偏微分 $\ppd{f}{x}$ を計算する際は、別途知っている座標系 $$ (x,y) $$ を使って $$ y $$ を固定する。
厳密な偏微分表記 $\Big( \ppd{f}{x} \Big)_y$ では、添字により座標系を補完していると見なせる。
これらに対し、逆基底表記では逆基底自体に座標系の情報を織り込んでいる状態と言える。

具体的に、 $\ffd{1}{dx}$ 自体に、正基底 $$ dx $$ の他に座標系情報 $$ (x,y) $$ も含まれる。
実際、 $\ffd{1}{dx}$ の値が対応する正基底のみならず、 $$ dy $$ も含めた全ての正基底に依存する。
その結果、微分は特定の座標系上で定義される演算と言える。

座標系から見た関数の微分

関数 $$ f $$ $$ = $$ $$ f(x,t) $$ で、かつ、 $$ x $$ $$ = $$ $$ x(t) $$ のとき、
常微分では関数を $$ f $$ $$ = $$ $$ f(t) $$ と見なして微分する。考えている座標系は１次元の $$ (t) $$ だけ。
偏微分では関数を $$ f $$ $$ = $$ と見なして微分する。考えている座標系は２次元の $$ (x,t) $$ 。
すなわち、常微分と偏微分は考えている座標系が異なると言える。

座標系間での文字衝突

座標系 $$ (t) $$ における逆基底 $\ffd{1}{dt}$ は１次元のために必ず対応する正基底 $$ dt $$ と平行である。
座標系 $$ (x,t) $$ における逆基底 $\ffd{1}{dt}$ は $$ dx $$ と直交するため、と平行する保障は無い*1。
このため、２つの座標系で正基底が同じでも逆基底 $\ffd{1}{dt}$ が異なりうる*2。

座標系明記による回避

回避手段として、まず考えられるのは厳密な偏微分 $\Big( \ppd{f}{t}\Big )_x$ のように座標系情報を補う表記。
凌宮数学では、補うべき情報は固定する変数ではなく、座標系と考えるため、
$\Big( \ddd{f}{t} \Big)_{x,t}$ のように座標系ごと補う。

*1 $\ffd{1}{dt}$ が $$ dt $$ と平行するのは、が他の全ての基底と直交する場合に限られる。
*2 この結論は、双対基底が座標系に依存することからも容易に理解できる。

文字の区別による回避

座標系に着目する立場を取る場合、
異なる座標系に異なる文字を用いれば座標系の明記は不要になる。

例えば、 $$ f $$ $$ = $$ $$ f(x(t), t) $$ に関しては、 $$ f $$ $$ = $$ $$ f(t) $$ $$ = $$ $f(x,\tau)$ と定義した上で $\tau$ $$ = $$ $$ t $$ とすれば良い。
ただし、 $$ t $$ $$ = $$ $\tau$ は等値の意味でしかなく、座標系は $$ (t) $$ と $(x,\tau)$ でしかなく、 $$ (x,t) $$ は不可。
この場合は常微分と偏微分は以下のようになり、簡易表記でも衝突しなくなる。

通常表記：*3	$\ddd{f}{t}$	$\ppd{f}{x}$ $\ddd{x}{t}$ $\ppd{f}{\tau}$ $\cancelto{1}{\ddd{\tau}{t}}\;\;$	$\ppd{f}{x}$ $\ddd{x}{t}$ $\ppd{f}{\tau}$
凌宮表記：*4	$\ddd{f}{t}$	$\ddd{f}{x}$ $\ddd{x}{t}$ $\ddd{f}{\tau}$ $\cancelto{1}{\ddd{\tau}{t}}\;\;$	$\ddd{f}{x}$ $\ddd{x}{t}$ $\ddd{f}{\tau}$

文字による座標系の書き分けでは、両方の表記において $\ddd{}{t}$ は座標系 $$ t $$ における微分、
$\ppd{}{\tau}$ や $\ddd{}{\tau}$ が座標系 $(x,\tau)$ における微分であることが良く分かる。

また、この書き分けは、 $$ f $$ $$ = $$ $$ f(x(t), y(t)) $$ について考え、
$$ y(t) $$ $$ = $$ $$ t $$ の場合も特別扱いせず $$ y $$ と $$ t $$ を区別していると理解しても良い。

*3 通常の厳密表記は $\ddd{f}{t}$ $$ = $$ $\Big(\ppd{f}{x}\Big)_\tau$ $\ddd{x}{t}$ $$ + $$ $\Big(\ppd{f}{\tau}\Big)_x$ $\cancelto{1}{\ddd{\tau}{t}}\;\;$
*4 凌宮の厳密表記は $\Big(\ddd{f}{t}\Big)_{t}$ $$ = $$ $\Big(\ddd{f}{x}\Big)_{x,\tau}$ $\Big(\ddd{x}{t}\Big)_t$ $$ + $$ $\Big(\ddd{f}{\tau}\Big)_{x,\tau}$ $\Big(\cancelto{1}{\ddd{\tau}{t}}\Big)_t$

ラグランジュ微分のオイラー表現

連続体力学では以下の２つの座標系が良く用いられる：

時間と独立な空間座標
粒子に着目した時間依存な物質座標

空間座標で考える場合、任意の物理量 $$ f $$ は位置 $\:x$ と時刻 $$ t $$ の関数 $f(\:x,t)$ として記述される。
物質座標で考える場合、時刻 $$ t=0 $$ のときの各粒子を初期位置 $\:\xi$ $$ = $$ $\:x|_{t=0}$ で表し、
任意の物理量 $$ f $$ を初期位置 $\:\xi$ と時刻 $$ t $$ の関数 $f(\:\xi,t)$ として記述する*5 *6。

各座標系における時間に関する偏微分は異なり、
それぞれオイラー微分（局所微分）とラグランジュ微分（物質微分）で呼び分ける。
オイラー微分は $\ppd{f}{t}$ $$ = $$ $\ppd{f(\:x,t)}{t}$ $$ = $$ $\Big( \ppd{f}{t} \Big)_{\:x}$ で定義され、通常は略式の偏微分で表記する。
ラグランジュ微分は $\ffd{Df}{Dt}$ $$ = $$ $\ppd{f(\:\xi,t)}{t}$ $$ = $$ $\Big( \ppd{f}{t} \Big)_{\:\xi}$ で定義され、専用の $\ffd{D}{Dt}$ で表記する*7。

ラグランジュ微分をオイラー表現で記述すると次のようになる：

$\ffd{Df}{Dt}$ $$ = $$ $\ppd{f}{t}$ $$ + $$ $\:v$ $\sx$ $\:\nabla f$

ただし、 $\:v$ $$ = $$ $\ppd{\:x(\:\xi,t)}{t}$ 、 $\:\nabla f$ $$ = $$ $\Big( \ppd{}{x},\ppd{}{y},\ppd{}{z} \Big) f$

これに対し、空間座標を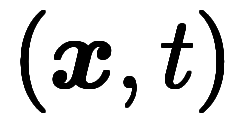 $(\:x,t)$ 、物質座標を 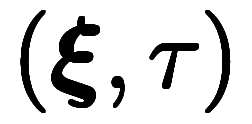$(\:\xi,\tau)$ と書き分けると、
ラグランジュ微分のオイラー表現は以下のように、座標変換が伴う連鎖則に帰着する。

$\ffd{Df}{D\tau}$	$\ppd{f}{t}$ $\:v$ $\sx$ $\:\nabla f$
$\ddd{f}{\tau}$	$\ddd{f}{t}$ $\ddd{\:x}{\tau}$ $\sx$ $\ddd{f}{\:x}$	$\ddd{f}{\:x}$ $\sx$ $\ddd{\:x}{\tau}$ $\ddd{f}{t}$ $\cancelto{1}{\ddd{t}{\tau}}\;\;$

*5 wikipedia／物質微分>https://ja.wikipedia.org/wiki/%E7%89%A9%E8%B3%AA%E5%BE%AE%E5%88%86
*6 地球流体電脳倶楽部／理論ノート／連続体の記述>https://www.gfd-dennou.org/arch/riron/renzoku/kijutu/pub/kijutu.pdf
*7 ラグランジュ微分を $\ddd{f}{t}$ で表記する流派もあるが、２次元 $(\xi,t)$ における偏微分であるため、
　　これは常微分ではなく、飽くまでも記号衝突を回避するための簡易表記でしかない。

回転座標系における相対微分

回転系の力学では以下の２つの正規直交座標系が良く用いられる：

時間と独立な絶対座標（慣性座標）
回転系に着目した時間依存な相対座標（回転座標）

回転系では、慣性座標系と回転座標系の２つの座標系が良く用いられる。
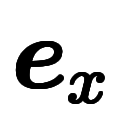
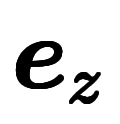
慣性座標系は、空間の基底 $\:e$ $$ = $$ $\langle$ $\:e_x$ $$ , $$ $\:e_y$ $$ , $$ $\:e_z$ $\rangle$ は時間 $$ t $$ に対し不変である。
回転座標系は、時間進行に伴い慣性座標系に対して角速度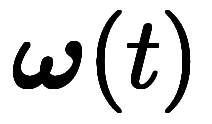 $\:\omega(t)$ で回転し、
空間の基底 $\:\varepsilon$ $$ = $$ $\langle$ $\:\varepsilon_x$ $$ , $$ $\:\varepsilon_y$ $$ , $$ $\:\varepsilon_z$ $\rangle$ と時間 $$ t $$ の関数となる*8。

各座標系における時間に関する微分は異なり、
それぞれ絶対導関数 $\ddd{}{t}$ と相対導関数 $\ddd{^\ast}{t}$ と区別される。
絶対導関数と相対導関数の間には「回転座標系の公式」という名のついた公式が存在する。

$\ddd{\:f}{t}$ $$ = $$ $\ddd{^\ast f}{t}$ $$ + $$ $\:\omega$ $\vx$ $\:f$

これに対し、慣性座標系の時空間を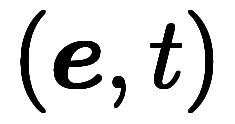 $(\:e,t)$ 、慣性座標系の時空間を 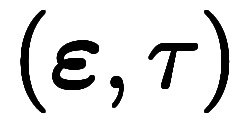$(\:\varepsilon,\tau)$ と書き分けると、
回転座標系の公式は以下のように、連鎖則に帰着する。

$\Big(\ddd{\:f}{t}\Big)_{\:e,\:t}$ $$ = $$ $\Big(\ddd{\:f}{\:\varepsilon}\Big)_{\:\varepsilon,\:tau}$ $\Big(\ddd{\:\varepsilon}{t}\Big)_{\:e,\:t}$ $$ + $$ $\Big(\ddd{\:f}{\tau}\Big)_{\:varepsilon,\:tau}$ $\Big(\cancelto{1}{\ddd{\:\tau}{t}}\Big)_{\:e,\:t}$