![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
����ˤ�����ʬ������ʬ�ζ��� |
���� |
| �������� |
������Ф������ֺ�ɸ��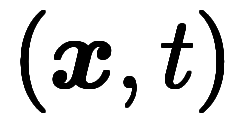 ��ʪ����ɸ��
��ʪ����ɸ��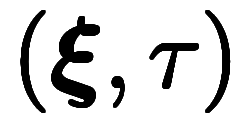 �Ƚ�ʬ����ȡ�
�Ƚ�ʬ����ȡ�
�饰�����ʬ�Υ����顼ɽ���ϰʲ��Τ褦�ˡ���ɸ�Ѵ���ȼ��Ϣ��§�˵��夹�롣
|
| |
|
|
|
 ��ɽ������ή�ɤ⤢�뤬��������
��ɽ������ή�ɤ⤢�뤬�������� �ˤ���������ʬ�Ǥ��뤿�ᡢ
�ˤ���������ʬ�Ǥ��뤿�ᡢ


��ž�Ϥ��ϳؤǤϰʲ��Σ��Ĥ�����ľ���ɸ�Ϥ��ɤ��Ѥ����롧
��ž�ϤǤϡ�������ɸ�ϤȲ�ž��ɸ�ϤΣ��Ĥκ�ɸ�Ϥ��ɤ��Ѥ����롣
������ɸ�Ϥϡ����֤δ���





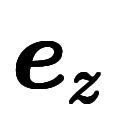
 �ϻ���
�ϻ��� ���Ф����ѤǤ��롣
���Ф����ѤǤ��롣
��ž��ɸ�Ϥϡ����ֿʹԤ�ȼ��������ɸ�Ϥ��Ф��Ƴ�®��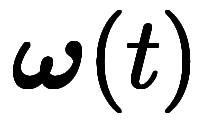 �Dz�ž����
�Dz�ž����
���֤δ���






 �Ȼ���
�Ȼ��� �δؿ��Ȥʤ롣
�δؿ��Ȥʤ롣
�ƺ�ɸ�Ϥˤ�������֤˴ؤ�����ʬ�ϰۤʤꡢ
���줾������Ƴ�ؿ� ������Ƴ�ؿ�
������Ƴ�ؿ� �ȶ��̤���롣
�ȶ��̤���롣
����Ƴ�ؿ�������Ƴ�ؿ��δ֤ˤϡֲ�ž��ɸ�Ϥθ����פȤ���̾�ΤĤ���������¸�ߤ��롣
|
������Ф���������ɸ�Ϥλ����֤�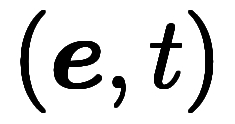 ��������ɸ�Ϥλ����֤�
��������ɸ�Ϥλ����֤�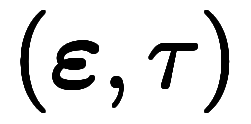 �Ƚ�ʬ����ȡ�
�Ƚ�ʬ����ȡ�
��ž��ɸ�Ϥθ����ϰʲ��Τ褦�ˡ�Ϣ��§�˵��夹�롣
|
|
|
|
|
�����ǡ�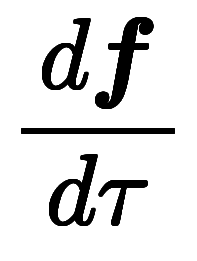 �ϲ�ž��ɸ�Ϥδ������������Ȥ���������ʬ�Τ�������Ƴ�ؿ��Ȥʤ롣
�ϲ�ž��ɸ�Ϥδ������������Ȥ���������ʬ�Τ�������Ƴ�ؿ��Ȥʤ롣
�ޤ���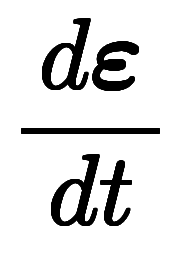 �ϲ�ž��ɸ�Ϥδ���λ�����ʬ�Ǥ��롣
�ϲ�ž��ɸ�Ϥδ���λ�����ʬ�Ǥ��롣
 ��������������
��������������
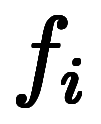
 ��ɽ����뤿��
��ɽ����뤿��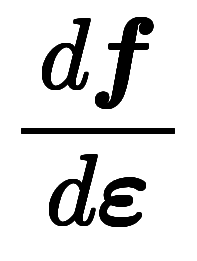 ��
�� �γ���ʬ
�γ���ʬ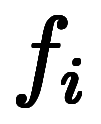 �Ǥ��롣
�Ǥ��롣
��������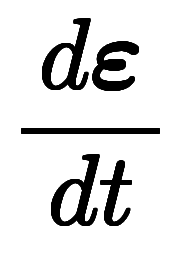

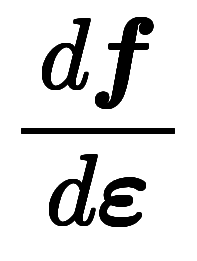 �������ˤϡ��ʲ��ι��פ�ɬ�פǤ��롣
�������ˤϡ��ʲ��ι��פ�ɬ�פǤ��롣
����ž�Ϥˤ�����®�٤��Ѱ̤����л�����ʬ�δط�����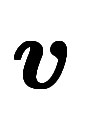



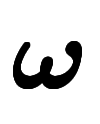

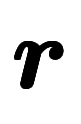 ��ꡢ
��ꡢ
Ǥ�դδ���٥��ȥ�ˤĤ���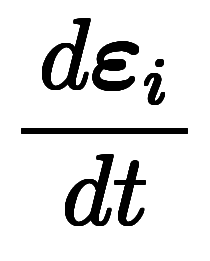

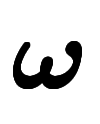

 ������Ω�ġ�
������Ω�ġ�
��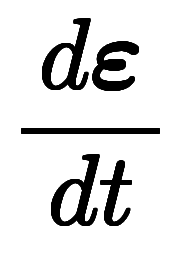 ��
��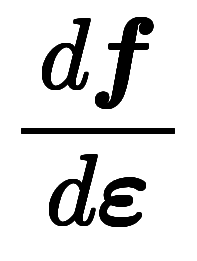 ���ɸ���¸�̤Ǥ��ꡢ
���ɸ���¸�̤Ǥ��ꡢ
 �λ����Ѳ�ʬ��
�λ����Ѳ�ʬ��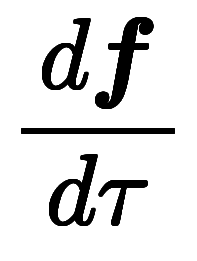 �ǹ�θ�����
�ǹ�θ�����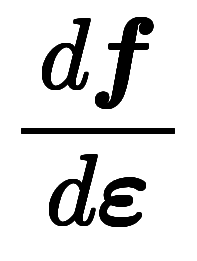 �Ϻ�ɸ�Ϥȶ��˲�ž����ʬ�����ʤ��ᡢ
�Ϻ�ɸ�Ϥȶ��˲�ž����ʬ�����ʤ��ᡢ
 ��
��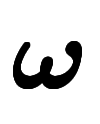 �Dz�ž�������к�ɸ�ʤ顢���θ�����Ǥ�դ�������ɤ���
�Dz�ž�������к�ɸ�ʤ顢���θ�����Ǥ�դ�������ɤ���
�������ǡ�����ľ��Ū�ˤ��뤿�ᡢ�ʲ��κ�ɸ�� ��Ƴ�����롧
��Ƴ�����롧
 ��
��  �θ�����ñ�̥٥��ȥ�
�θ�����ñ�̥٥��ȥ�

 ��
�� ��
��  ��
��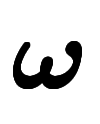 �ο�ľ������ñ�̥٥��ȥ�
�ο�ľ������ñ�̥٥��ȥ�

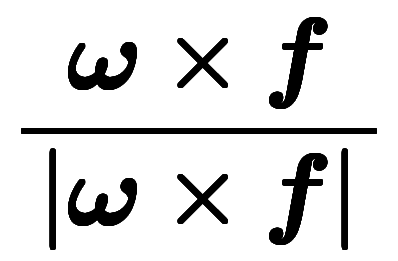 ��
�� ��
��  ��
�� �ο�ľ������ñ�̥٥��ȥ�
�ο�ľ������ñ�̥٥��ȥ�



 *8��
*8��������ȡ�


 �Ƚ�
�Ƚ�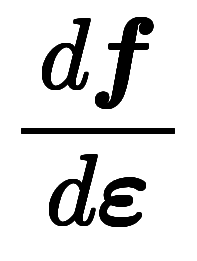 ��
�� ��ʬ�ʳ���
��ʬ�ʳ��� �Ȥʤ롣
�Ȥʤ롣
���Τ��ᡢ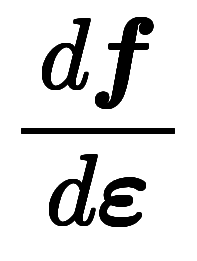 �����Ѥ���
�����Ѥ���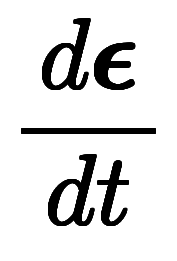 ��
�� ��ʬ�����ͤ�����ɤ���
��ʬ�����ͤ�����ɤ���
���ʤ����
|
|
| |
| |
|
�ʾ��ꡢ
|
|
|



��ʬ�Ϻ�ɸ�Ϥ��꤭�α黻�Ǥ��뤿�ᡢ��ɸ�Ϥ����ʬ������֤ˤ��Ƥ���ɬ�פ����롣
���̤ˡ�����ʬ�θ�̩ɽ���ǤϤ��ξ�郎���ꥢ����Ƥ��롣
�Ф��ơ��ʰ�ɽ���Ǥ��̾���ʬ������Ѥ��ƽ�ʬ���뤬��
ο�ܿ��ؤǤϺ�ɸ�Ϥ�ռ����ơ��ۤʤ��ɸ�Ϥ˰ۤʤ�ʸ���ǽ�ʬ�����������Ѥ��롣
������Ǥϡ�Ϣ³���ϳؤΥ饰�����ʬ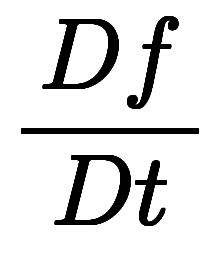 ���ž���ϳؤ�������ʬ
���ž���ϳؤ�������ʬ ���Ф���
������
��ɸ����˻��֤�ɽ���ѿ��� ��
��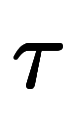 �˽�ʬ������
�˽�ʬ������
�������ü����ʬ�ϡ����줾���������ɸ�Ͼ�Ǥλ�����ʬ��ª����줿��