![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
偏微分 のバックアップの現在との差分(No.1) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
偏微分 のバックアップの現在との差分(No.1) |
|
一般に、1変数関数 対して、2変数関数 この 導入教科書的に微分をまとめると、大まか次のようになる:
1変数関数
2変数関数
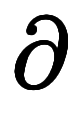 を使った偏微分と区別して、 を使った偏微分と区別して、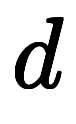 を使った微分を特に常微分と言う。これだけの定義だが、偏微分と常微分の違いを正しく説明できる人は意外に少ない。勿論、「偏微分では を使った微分を特に常微分と言う。これだけの定義だが、偏微分と常微分の違いを正しく説明できる人は意外に少ない。勿論、「偏微分では を固定している」だけでは矛盾が生じる。実際、学ぶ方にとっては を固定している」だけでは矛盾が生じる。実際、学ぶ方にとっては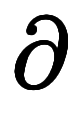 と と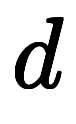 の使い分けが非常に紛らわしく、微分が難しく感じる要因の一つである。結論を言うと、偏微分と常微分は同じ微分演算であるため、微分としては共通の記号を通して使うべき。しかし、偏微分と言うだけで、積分は勿論、既にベクトルまで含まれるのが現状である。このため、表記を統合するためには、記号の意味から変える必要がある。以下では、まず同一関数 の使い分けが非常に紛らわしく、微分が難しく感じる要因の一つである。結論を言うと、偏微分と常微分は同じ微分演算であるため、微分としては共通の記号を通して使うべき。しかし、偏微分と言うだけで、積分は勿論、既にベクトルまで含まれるのが現状である。このため、表記を統合するためには、記号の意味から変える必要がある。以下では、まず同一関数 に対し、偏微分 に対し、偏微分 と常微分 と常微分 が同時に存在し、異なる値を持つ場合について考える。次ぎに、 が同時に存在し、異なる値を持つ場合について考える。次ぎに、 で欠けてる情報を補った偏微分のフル表記とその意味について考える。最後に、偏微分の意味毎の分離表記について考え、偏微分と常微分を統合する。この話しの目標は、関数 で欠けてる情報を補った偏微分のフル表記とその意味について考える。最後に、偏微分の意味毎の分離表記について考え、偏微分と常微分を統合する。この話しの目標は、関数 があって、どんな関数だろうと があって、どんな関数だろうと で微分する限り で微分する限り と表記することである。 と表記することである。
目次
|
||||||||||||||