![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
1階線形常微分方程式 |
|
|
定数係数: |
変数係数: |
暗記さえできれば、定数係数で1階の線形な常微分方程式に関しては、必ず解けることになる。
しかし問題は、丸暗記では前後に習得する知識と繋がらず、全体を効率良く学べない。
特に、直後に学ぶ定数係数2階線形常微分方程式は、1階を応用で簡単に解けてしまう。
これらに対し、凌宮数学では、2階ないし 階の線形常微分方程式に繋がるような、
階の線形常微分方程式に繋がるような、
学習済み知識に基づいた1階線形常微分方程式のもう少し考え易い解き方を与える。






一般に、ある関数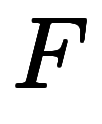

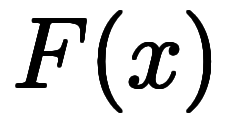 の常微分
の常微分 が分かれば、不定積分で解けることが分かっている*3。
が分かれば、不定積分で解けることが分かっている*3。
|




 の場合は、左辺
の場合は、左辺

 を
を に纏めらると、積分で解ける。
に纏めらると、積分で解ける。
そのため、まずは

 の「
の「 」を消したい。
」を消したい。



「 」を消すには、等号の片方に「
」を消すには、等号の片方に「 」が1つ、他方に「
」が1つ、他方に「 」が無い公式が必要である。
」が無い公式が必要である。
高校範囲で探す限り、等号の左右で「 」の数が異なるのは積の微分しかない*5:
」の数が異なるのは積の微分しかない*5:
しかし、



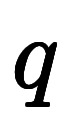 を
を

 と比較しても、
と比較しても、
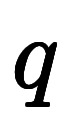

 が嵌るものの、
が嵌るものの、

 と
と

 を同時に満たす
を同時に満たす は存在しない*7。
は存在しない*7。
このため、



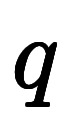 に嵌るように、
に嵌るように、

 を調節する必要がある。
を調節する必要がある。



上記の試算は

 の縛りが厳しすぎるため、
の縛りが厳しすぎるため、

 となり、
となり、

 を満せなくなっている。
を満せなくなっている。
そのため、例えば

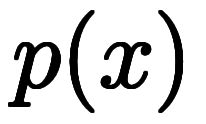 と自由にすれば、
と自由にすれば、 を
を の方の条件に合わせば解ける。
の方の条件に合わせば解ける。
 の係数を
の係数を にするには、単純に全ての項に
にするには、単純に全ての項に を掛ければ良い:
を掛ければ良い:
|
一般に、積分するために掛ける関数 を積分因子、積分因子を掛ける手法を積分因子法と呼ぶ。
を積分因子、積分因子を掛ける手法を積分因子法と呼ぶ。
積分因子法は、微分関係を比較的自由に調節できるため、微分方程式に良く利く。




 を
を



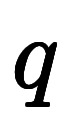 と比較すると、
と比較すると、

 なる
なる を探せば良いことが分かる。
を探せば良いことが分かる。
幸い、これは変数分離形という易しい類の微分方程式であるため、簡単に求まる:
|
|
⇔ | 変数分離 |
⇔ | 不定積分 |
⇔ | 積分実行、原始関数を |
⇔ | 両辺で指数を取る |
⇔ | 指数法則で定数部を分離 |
今、 は
は
 を満たせば良いので、以降では簡単そうな
を満たせば良いので、以降では簡単そうな を積分因子に選ぶ。
を積分因子に選ぶ。
定数係数の場合は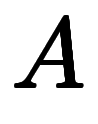









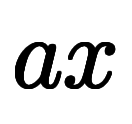 になり、積分因子は
になり、積分因子は となる。
となる。



以上で解く筋道が通る:
この筋道を逆から書けば「解答」となる:
| 原方程式 |
⇔ | 両辺に積分因子 |
⇔ | 積の微分に嵌める(不定積分を実行) |
⇔ | 1つの微分に纏める(部分積分を実行) |
⇔ | 積分する |
⇔ | 両辺に |



原方程式 は、
は、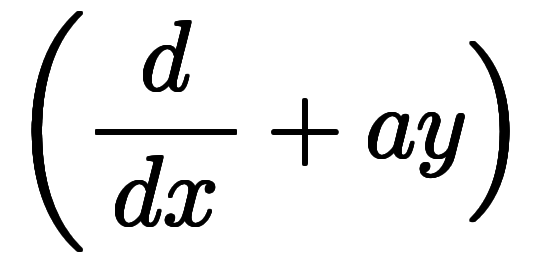

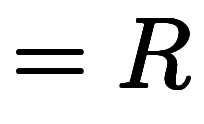 と括れば、
と括れば、
未知関数 から既知関数
から既知関数 を求める少々複雑な微分演算にも見える。
を求める少々複雑な微分演算にも見える。
以下のように1階線形常微分演算子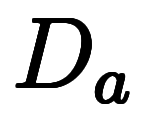 を定義すると、演算
を定義すると、演算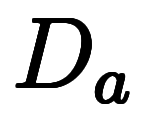 と演算対象
と演算対象 に明示的に分離できる。
に明示的に分離できる。
1階線形常微分演算子: |
1階線形常微分方程式: |


