![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
1次元ベクトル |
|
大学では、2次元、3次元と 勿論、1次元のベクトルはスカラで、高校まで完璧に勉強している、などと期待してはならない。 こうして、高校と大学のギャップに嵌まる学生が量産される。 凌宮数学では、このギャップを埋めるため、小学校で学ぶ数直線から出発する。 数直線=1次元の座標系
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
| 表1: 座標とベクトルの対応関係 | |
|---|---|
| 座標用語 | ベクトル用語 |
| 座標 | ベクトル |
| 座標軸 | 基底 |
| 座標値 | 成分 |
座標軸は無限に長い矢印だったが、ベクトルでは基底と呼ばれる長さが有限な矢印に置き換わる。
基底の向きは座標の向き、基底の長さで座標の間隔を表していると考えて良い。
この他、成分は座標値にそのまま対応する。
高校では座標軸も任意の座標値も同じ文字( や
や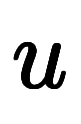 )を使っていたが、
)を使っていたが、
ベクトルでは基底も成分も同じ式に書き込むため、同じ記号は使えない。
一般に成分は のままに、基底には
のままに、基底には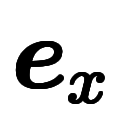 など別の記号を当てる*3。
など別の記号を当てる*3。
図2と図3の読み替えを纏めると、表2となる。
| 表2: 図2と図3の読み替え | |||||
|---|---|---|---|---|---|
| 座標 | ベクトル | 座標 | ベクトル | 任意座標 | 任意ベクトル |
 軸での 軸での![\iro[md]{1} $$ \iro[md]{1} $$](./eq/eq-ni-bd6d527c0da6491ed080fd967a3c711e.png) | 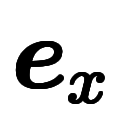 |  軸での 軸での![\iro[md]{2} $$ \iro[md]{2} $$](./eq/eq-ni-6d289f26e86c2261cd3c4e267c4ca43c.png) | 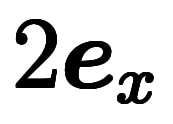 |  軸での 軸での | 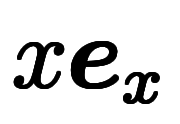 |
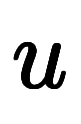 軸での 軸での![\iro[mz]{1} $$ \iro[mz]{1} $$](./eq/eq-ni-8a983aa1e281e7534d776c4e2663763d.png) |  | 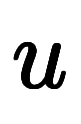 軸での 軸での![\iro[mz]{4} $$ \iro[mz]{4} $$](./eq/eq-ni-bfd77acdf7167eef5daf2e216fe091ed.png) | 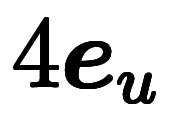 | 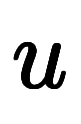 軸での 軸での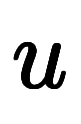 | 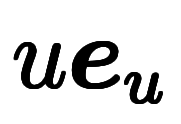 |
基底は座標軸を表すと同時に、それぞれの軸での が表す座標に対応したベクトルでもある。
が表す座標に対応したベクトルでもある。
他の座標は、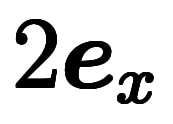 や
や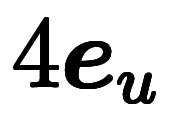 のように、成分と基底を掛け合わせて表す
のように、成分と基底を掛け合わせて表す
同様に、任意の座標は、任意の座標値を基底に掛け表せた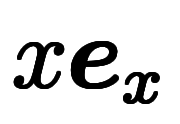 と
と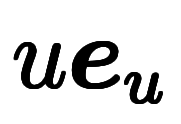 になる。
になる。
また、ベクトルでは座標系に依らない座標にベクトル記号を与えている。
図3の例では、青線の右端を表すベクトル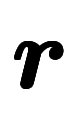 がベクトル記号である。
がベクトル記号である。
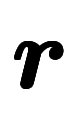 は
は も
も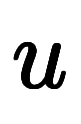 も関係なく、
も関係なく、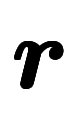 である。
である。
図3のベクトルを使えば「![\iro[md]{x} $$ \iro[md]{x} $$](./eq/eq-ni-ed85b00cae4c14904b2b4dbe5158adac.png) 軸での
軸での![\iro[md]{x} $$ \iro[md]{x} $$](./eq/eq-ni-ed85b00cae4c14904b2b4dbe5158adac.png) と
と![\iro[mz]{u} $$ \iro[mz]{u} $$](./eq/eq-ni-e550e453a70b39dd61c397dc3c71501e.png) 軸での
軸での![\iro[mz]{u} $$ \iro[mz]{u} $$](./eq/eq-ni-e550e453a70b39dd61c397dc3c71501e.png) が同じ座標である」ということは、次のように書ける。
が同じ座標である」ということは、次のように書ける。
|
座標関係の言葉に直訳すると「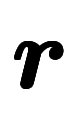 の座標は、
の座標は、![\iro[md]{x} $$ \iro[md]{x} $$](./eq/eq-ni-ed85b00cae4c14904b2b4dbe5158adac.png) 軸での
軸での 、
、![\iro[mz]{u} $$ \iro[mz]{u} $$](./eq/eq-ni-e550e453a70b39dd61c397dc3c71501e.png) 軸での
軸での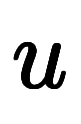 と同じ」になる。
と同じ」になる。
ベクトルの言葉に直訳すると「ベクトル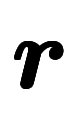 は、基底
は、基底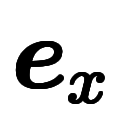 と成分
と成分 の掛け合わせ、、基底
の掛け合わせ、、基底 と成分
と成分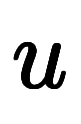 の掛け合わせと同じ」になる。
の掛け合わせと同じ」になる。
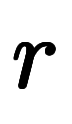

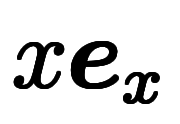

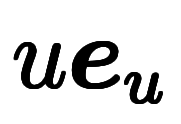 について、これを以下のように式変形できる。
について、これを以下のように式変形できる。
| 表3: ベクトル、基底、成分の相互変換式 | |||
|---|---|---|---|
| ベクトルを求める式 | 基底を求める式 | 成分を求める式 | |
 軸について 軸について | 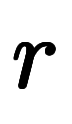  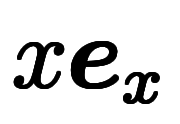 | 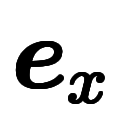 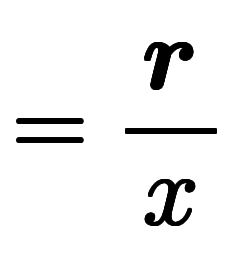 |  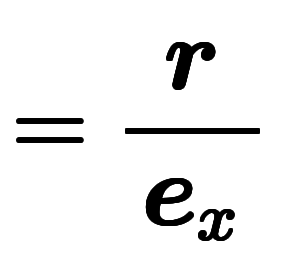 |
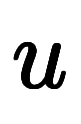 軸について 軸について | 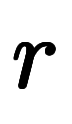  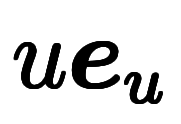 |   | 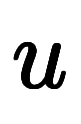  |
ベクトルを求める式は、大学の教科書であれば良く見かける。
これに対し、基底を求める式と成分を求める式は全く見当たらないはずである。
それは、1次元ベクトルが教えられないのと、2次元から姿が変ってしまうためである。
そもそも、ベクトルを求める式が小学校から学ぶような乗算で済むのも座標系が1次元で、座標軸が直線で、座標軸が等間隔とう厳しい条件が全て成り立つときに限る。
ベクトルを求める式だけが、乗算で無くなっても書き方は変えず、計算規則を変えて対応している。
書き方を変えないお陰で、乗算が成り立たない場合も公式の姿が変わらず、新しく覚える必要はない。
残念なことに、基底を求める式と成分を求める式は、書き方が統一されてない。
例えば、成分を求める式は、ありえないベクトルの割るベクトルになるのが容易に想像できる。
しかし、割り算でも書き方を変えなければ、公式の姿が変らず、多くの公式を覚えずに済む。
以上の理由により、凌宮数学ではの成分を求める式の姿を変えずに貫き続ける。
ただし、基底を求める式では、成分だけで基底を復元するには、スカラの成分が持つ情報が少ない過ぎるため、2次元以上では定義できない。