![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
łä»»É®»»¤Î˛áÉÔÂÂбţ |
ÇŘ·Ę |
| ||
| ||
|
| |
| ¤Ţ¤ş¤Ď57ˇá19ˇß3¤ň°ú¤Ż | |
| 49ˇä19¤ÇÉÔ | |
| ÄɲäÇ38ˇá2ˇß19¤ň°ú¤Ż | |
| ||
| 38¤Ď̵¤¤¤«¤éˇ˘¤Č¤ę¤˘¤¨¤ş76ˇá19ˇß4¤ň°ú¤Ż | |
| 35ˇä19¤ÇÉÔ¡˘38¤â̵¤¤¤«¤é19¤ň1¤Ä°ú¤±¤Đ¤ę¤ë | |
| 16ˇá35ˇÝ19¤Č°ú¤¤¤Ćˇ˘8¤ň˛·¤ą | |
| 168ˇă171¤Ç˛áľęˇ˘¤Č¤ę¤˘¤¨¤ş˛ľŔѤ«¤é19¤ň1¤Ä¸ş¤é¤ą | |
| 171ˇÝ19ˇá152¤Č°ú¤¤¤Ćˇ˘˝¤Ŕµ¤·¤żÍľ¤ę168¤«¤é152¤ňÉáÄ̤˰ú¤Ż | |
|
¤č¤Ă¤Ćˇ˘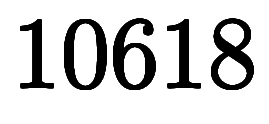 ˇŕ
ˇŕ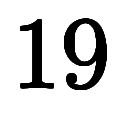 ˇá
ˇá ˇÜ
ˇÜ






¤Ţ¤şˇ˘ÍѸě¤ÎŔâĚŔ¤ň·ó¤Í¤Ćˇ˘˛áÉÔ¤Î̵¤¤ÍýÁŰĹŞ¤Ęłä»»É®»»¤ňłÎǧ¤ą¤ëˇŁ
| ˇ ¤Č¤ę¤˘¤¨¤ş˛ľľ¦¤ň5¤ČĂÖ¤Ż | |
|
| |
| ˘ ¤Č¤ę¤˘¤¨¤ş˛ľŔŃ95ˇá˝üżô19ˇß˛ľľ¦¤ň·×»» | |
| Ł Čď˝üżô¤«¤é˛ľŔѤň°ú¤ˇ˘0ˇă˛ľÍľ11ˇă˝üżô19¤Î˛áÉÔÂ̵¤·¤ÇłÎÄę | |
| ˇˇˇˇłÎÄꤷ¤żÍľ¤ę¤ËČďľčżô¤«¤é1·ĺąß¤í¤·¤ĆČďľčżô¤ňż·¤ż¤Ëşî¤Ă¤Ć·ŃÂł | |
| ||
| ||
|
ĹÓĂ桢
ˇˇˇˇˇ¦ °ú¤¤¤ż·ë˛Ě¤¬˛ľÍľˇä˝üżô¤Îľěąç¤ĎÉÔ¡˘
ˇˇˇˇˇ¦ ˛ľŔѡäČďľčżô¤Ç°ú¤±¤Ę¤¤ˇ˘¤Ä¤Ţ¤ęˇ˘°ú¤¤¤Ć¤â˛ľÍľˇă0¤Ë¤Ę¤ëľěąç¤Ď˛áľęˇ˘
Ŕµ¤·¤¤ľ¦¤ňĆŔ¤ë¤ż¤á¤Ë¤Ďˇ˘˛ľľ¦¤ň˝¤Ŕµ¤ą¤ëɬÍפ¬Ŕ¸¤¸¤ëˇŁ



| Ą˛ľľ¦4¤ňĽĐŔţ¤ÇľĂ¤·ˇ˘ľ¦¤ň1¤ÄÂż¤¤5¤Ë˝¤Ŕµ | |
| ˇ ¤Č¤ę¤˘¤¨¤ş˛ľľ¦¤ň4¤ČĂÖ¤Ż | |
|
| |
| ˘ ¤Č¤ę¤˘¤¨¤ş˛ľŔŃ19ˇß4¤ň·×»» | |
| Ł ¤Č¤ę¤˘¤¨¤ş106¤«¤é76¤ň°ú¤¤¤Ćˇ˘˛ľÍľ30ˇä19¤ÇÉÔ¤ňłÎǧ | |
| ¤ ˛ľÍľ¤ňĽĐŔţ¤ÇľĂ¤·ˇ˘Íľ¤ę¤ň˛ľÍľ¤«¤é˝üżô¤ň°ú¤¤¤ż·ë˛Ě¤Ë˝¤Ŕµ |



ÉÔ¤ʾěąç¤ĎÍľ¤ę¤ň˝¤Ŕµ¤ą¤ě¤ĐÎɤ¤¤¬ˇ˘
˛áľę¤Ęľěąç¤ĎÉé¤ÎÍľ¤ę¤ň˛óČň¤ą¤ë¤ż¤á¤Ë¤Ďˇ˘˛ľŔѤň˝¤Ŕµ¤ą¤ë¤ł¤Č¤Ë¤Ę¤ëˇŁ
| ¤˛ľľ¦6¤ňĽĐŔţ¤ÇľĂ¤·ˇ˘1¤ÄľŻ¤Ę¤¤5¤Ë˝¤Ŕµ | |
| ˇ ¤Č¤ę¤˘¤¨¤ş˛ľľ¦¤ň6¤ČĂÖ¤Ż | |
|
| |
| ˘ ¤Č¤ę¤˘¤¨¤ş˛ľŔŃ19ˇß6¤ň·×»»¤·ˇ˘114ˇä106¤Ç˛áľę¤ňłÎǧ | |
| Ł ˛ľŔѤňĽĐŔţ¤ÇľĂ¤·ˇ˘˛ľŔѤ«¤éľčżô¤ň°ú¤¤¤żżô¤Ë˝¤Ŕµ | |
| Ą Čď˝üżô¤«¤é˝¤Ŕµ¸ĺ¤ÎŔѤň°ú¤ˇ˘11ˇă19¤ňłÎǧ |



Íפϣ±ÇÜÉÔ¤·¤żľěąç¤ÎϢ³Ŭ±ţˇŁ
ĽÂĽÁľĺˇ˘ŔčƬŁ±·ĺ¤Č¶ĺ¶ĺ¤Çľ¦¤ňÂçÂΡޣ±¤ÎČϰϤËÍޤ¨¤é¤ě¤ë¤ż¤áˇ˘
±ż°¤ŻŁ˛ÇÜÉÔ¤·¤ż¤Č¤¤Ë¤â¤¦°ě˛ó°ú¤¤¤ä¤ë¤«ˇĽ¤Č¤¤¤¦´¶łĐ¤ÇÎɤ¤ˇŁ
| Ą˛ľľ¦3¤ňĽĐŔţ¤ÇľĂ¤·ˇ˘ľ¦¤ň2¤ÄÂż¤¤5¤Ë˝¤Ŕµ | |
| ˇ ¤Č¤ę¤˘¤¨¤ş˛ľľ¦¤ň3¤ČĂÖ¤Ż | |
|
| |
| ˘ ¤Č¤ę¤˘¤¨¤ş˛ľŔŃ19ˇß3¤ň·×»» | |
| Ł ¤Č¤ę¤˘¤¨¤ş106¤«¤é57¤ň°ú¤¤¤Ćˇ˘˛ľÍľ49ˇä19¤ÇÉÔ¤ňłÎǧ | |
| Ł ˛ľÍľ¤ňĽĐŔţ¤ÇľĂ¤·ˇ˘˛ľÍľ¤«¤é˝üżô19¤ň°ú¤¤¤ŻˇŁ | |
| ¤ ˛ľÍľ¤ňĽĐŔţ¤ÇľĂ¤·ˇ˘ąą¤Ë˝üżô19¤ň°ú¤¤¤Ćˇ˘11ˇă19¤ňłÎǧˇŁ |



Ł±Çܲáľę¤·¤żľěąç¤ÎϢ³Ŭ±ţˇŁ
Čďľčżô¤«¤é˛ľŔѤň°ú¤±¤ë¤Ţ¤Çˇ˘˛ľŔѤ«¤é˝üżô¤ň°ú¤Âł¤±¤ĐÎɤ¤ˇŁ
| Ą˛ľľ¦7¤ňĽĐŔţ¤ÇľĂ¤·ˇ˘2˛ó°ú¤¤¤ż¤Î¤Ç2ľŻ¤Ę¤¤5¤Ë˝¤Ŕµ | |
| ˇ ¤Č¤ę¤˘¤¨¤ş˛ľľ¦¤ň7¤ČĂÖ¤Ż | |
|
| |
| ˘ ¤Č¤ę¤˘¤¨¤ş˛ľŔŃ19ˇß7¤ň·×»»¤·ˇ˘˛ľÍľ133ˇä106¤Ç˛áľę¤ňłÎǧ | |
| Ł ˛áľę¤Ę¤ó¤Çˇ˘˛ľŔѤ«¤é˝üżô¤ň°ú¤Ż | |
| ¤ ¤Ţ¤Ŕ˛áľę¤Ę¤ó¤Çˇ˘ąą¤Ë˝üżô¤ň°ú¤ˇ˘95ˇă106¤Ç°ú¤±¤ë¤ł¤Č¤ňłÎǧ | |
| ¦ 106¤«¤é˝¤Ŕµ¤·¤ż˛ľŔŃ95¤ň°ú¤ˇ˘11ˇă19¤Ç˛áÉÔÂ̵¤·¤ňłÎǧ |



Ŕµ¤·¤¤ľ¦¤ňĹö¤Ć¤ëĹŘÎϤ·¤Ć¤ě¤ĐˇŢ1¤ËÍޤ¨¤é¤ě¤ë¤¬ˇ˘
ĂĽ¤«¤éĹö¤Ć¤č¤¦¤Č¤»¤şˇ˘2Çܤä3Çܡ˘5Çܤʤɷ׻»¤·¤ä¤ą¤¤żô¤Ç˛Ă¸ş¤ą¤ëşîŔď¤âĽÂÍŃĹŞ¤Ç¤˘¤ëˇŁ
¤˝¤Îľěąçˇ˘˝¤Ŕµ¤¬Â礤Ż¤Ę¤ę¤¦¤ë¤ż¤áˇ˘ÄɲäDzľŔѤň˛Ă¸ş¤ą¤ëĽęˡ¤¬»Č¤¨¤ëˇŁ
| ¤˛ľľ¦3¤ňĽĐŔţ¤ÇľĂ¤·ˇ˘2ÇÜÂż¤¤5¤Ë˝¤Ŕµ | |
| ˇ ¤Č¤ę¤˘¤¨¤ş˛ľľ¦¤ň3¤ČĂÖ¤Ż | |
|
| |
| ˘ ¤Č¤ę¤˘¤¨¤ş˛ľŔŃ19ˇß3¤ň·×»» | |
| Ł ¤Č¤ę¤˘¤¨¤ş106¤«¤é57¤ň°ú¤¤¤Ćˇ˘˛ľÍľ49ˇä19¤ÇÉÔ¤ňłÎǧ | |
| Ą ÄɲäDzľŔŃ19ˇß2¤ň·×»» | |
| ¦ ˛ľÍľ¤«¤éÄɲäβľŔѤň°ú¤ˇ˘11ˇă19¤Ç˛áÉÔÂ̵¤·¤ňłÎǧ |



˛ľľ¦¤¬˛áľę¤·¤żľěąçˇ˘¤Č¤ę¤˘¤¨¤ş°ú¤¤¤Ć¤ĎÍľ¤ę¤¬Éé¤Ë¤Ę¤ëˇŁ
¤ż¤Ŕˇ˘·ÁĽ°ľĺ¤Ç¤Ď˛Ľ¤«¤éľĺ¤ňµŐ¤Ë°ú¤±¤Đˇ˘ÄĚľď¤Î¸ş»»¤ÎÉ®»»¤ÎĽę˝ç¤ÇşŃ¤ŕˇŁ
¤Ţ¤żˇ˘Éé¤ÎÍľ¤ę¤Î˝¤Ŕµ¤Ë˛ľŔѤň˛Ă¤¨¤ë¤¬ˇ˘¤ł¤ě¤â˛Ľ¤«¤éľĺ¤ňµŐ¤Ë°ú¤Ż¸ş»»¤ÇşŃ¤ŕˇŁ
| ¤˛ľľ¦7¤ňĽĐŔţ¤ÇľĂ¤·ˇ˘2ÇÜľŻ¤Ę¤¤5¤Ë˝¤Ŕµ | |
| ˇ ¤Č¤ę¤˘¤¨¤ş˛ľľ¦¤ň7¤ČĂÖ¤Ż | |
|
| |
| ˘ ¤Č¤ę¤˘¤¨¤ş˛ľŔŃ19ˇß7¤ň·×»»¤·ˇ˘˛ľÍľ133ˇä106¤Ç˛áľę¤ňłÎǧ | |
| Ł ¤Č¤ę¤˘¤¨¤şµŐ¤Ë133¤«¤é106¤ň°ú¤Ż | |
| Ą ÄɲäDzľŔŃ19ˇß2¤ň·×»» | |
| ¦ ÄɲäβľŔѤ«¤é˛ľÍľ¤ňµŐ¤Ë°ú¤ˇ˘11ˇă19¤Ç˛áÉÔÂ̵¤·¤ňłÎǧ |
Îă¤Ç¤Ďˇ˘106¤¬Íľ¤ęˇ˘133¤¬˛ľŔѡ˘38¤¬ĘäŔµ¤Çˇ˘·ë¶É¤Ď106ˇÝ133ˇÜ38ˇá11¤ň·×»»¤·¤Ć¤¤¤ë¤¬ˇ˘
µŐ°ú¤¤Ë¤č¤Ă¤Ć·ÁĽ°ľĺ¤Ç¤Ď38ˇÝˇĘ133ˇÝ106ˇËˇá11¤Čˇ˘Éé¤Îżô¤ň°·¤ď¤Ę¤¤Áŕşî¤Ë¤Ę¤Ă¤Ć¤¤¤ëˇŁ
¤Ţ¤żˇ˘·×»»ĹÓĂć¤Ç¤ĎÉé¤ÎÍľ¤ę¤¬¸˝¤ě¤ë¤¬ˇ˘¸˝¤ě¤ëÍľ¤ę¤ĎÁ´¤Ć˝üżôÇܰ㤤¤Ç¤˘¤ë¤ż¤áˇ˘
¤ł¤ě¤ĎÉé¤Îżô¤Î˝üÍľ¤Ř¤ÎĽ«Áł¤ĘłČÄĄ¤Č¤Ę¤Ă¤Ć¤¤¤ëˇŁ



B+2¤Ç¤ĎÉé¤ÎÍľ¤ę¤ËÂФ·ˇ˘µŐ°ú¤¤ÇÉé¤Îżô¤ň°·¤ď¤ş¤ËşŃ¤Ţ¤»¤Ć¤¤¤ë¤¬ˇ˘
ĽÂ¤Ďˇ˘ĘäżôÉ˝¸˝¤ň»Č¤¨¤Đˇ˘¤˝¤Î¤Ţ¤Ţľĺ¤«¤é°ú¤¤¤Ć¤âŔµ¤·¤¤Ĺú¤¨¤ň˝Đ¤»¤ëˇŁ
¤ż¤Ŕ¤·ˇ˘ĘäżôÉ˝¸˝¤Ď°ěČĚĹŞ¤Ç¤Ď¤Ę¤¤¤Î¤Çˇ˘¤ł¤ÎĘýˡ¤ĎĽÂşÝ»Č¤ď¤ě¤ë¤ł¤Č¤Ď¤Ę¤¤*1ˇŁ
| ¤˛ľľ¦7¤ňĽĐŔţ¤ÇľĂ¤·ˇ˘2ÇÜľŻ¤Ę¤¤5¤Ë˝¤Ŕµ | |
| ˇ ¤Č¤ę¤˘¤¨¤ş˛ľľ¦¤ň7¤ČĂÖ¤Ż | |
|
| |
| ˘ ¤Č¤ę¤˘¤¨¤ş˛ľŔŃ19ˇß7¤ň·×»»¤·ˇ˘˛ľÍľ133ˇä106¤Ç˛áľę¤ňłÎǧ | |
| Ł ¤Č¤ę¤˘¤¨¤ş106¤«¤é133¤ň°ú¤Żˇ˘ĚµÍý¤ä¤ę°ú¤ŻˇŁľÜşŮ¤Ď¸ĺ˝ŇˇŁ | |
| Ą ÄɲäDzľŔŃ19ˇß2¤ň·×»» | |
| ¦ ĘäŔµ¤Î˛ľŔѤňÉáÄ̤ˤąˇ˘11ˇă19¤Ç˛áÉÔÂ̵¤·¤ňłÎǧ |



ĹÓĂć¤Ç˝Đ¤Ć¤Ż¤ë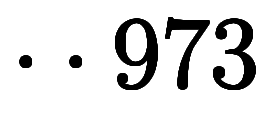 ¤¬B+2¤Ç˝Đ¤·¤ż
¤¬B+2¤Ç˝Đ¤·¤ż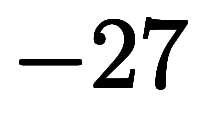 ¤Î10¤ÎĘäżôÉ˝¸˝*2¤Ç¤˘¤ëˇŁ
¤Î10¤ÎĘäżôÉ˝¸˝*2¤Ç¤˘¤ëˇŁ
¤ł¤Î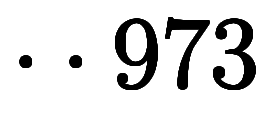 ¤Ď
¤Ď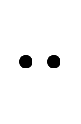
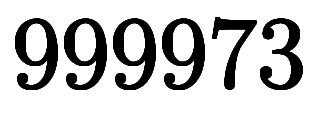 ¤Î¤č¤¦¤Ëľĺ°Ě¤Ë
¤Î¤č¤¦¤Ëľĺ°Ě¤Ë ¤¬Ěµ¸Â¤ËÂł¤ŻÉ˝µˇŁ
¤¬Ěµ¸Â¤ËÂł¤ŻÉ˝µˇŁ
¤˝¤Î ¤Ďˇ˘ĚµÍý¤ä¤ę°ú¤ŻşÝ¤ËČŻŔ¸¤·¤żĚµ¸Â¤Î·«˛Ľ¤¬¤ę¤Î·ë˛ĚˇŁ
¤Ďˇ˘ĚµÍý¤ä¤ę°ú¤ŻşÝ¤ËČŻŔ¸¤·¤żĚµ¸Â¤Î·«˛Ľ¤¬¤ę¤Î·ë˛ĚˇŁ
| Ą¤ł¤¦¤·¤Ćˇ˘ľĺ°Ě¤«¤é10ĽÚ¤ę¤Ćˇ˘˛Ľ°Ě¤Ë1Âߤą·ë˛Ěˇ˘9¤¬ÎĚ»ş¤µ¤ě¤ë |
| ˇ 106¤Îľĺ°Ě¤Ë0¤¬Ěµ¸Â¤ËÂł¤¤¤Ć¤¤¤ë |
| ˘ ˝˝¤Î°Ě¤Î0ˇÝ3¤Î»ţĹŔ¤Ç·«¤ę˛Ľ¤˛¤¬ČŻŔ¸¤·ˇ˘106¤Î1¤¬0¤Ë¤Ę¤ë |
|
¸ˇ»»¤Č¤·¤Ćˇ˘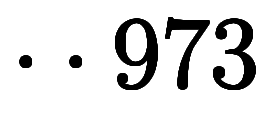 ¤Ë
¤Ë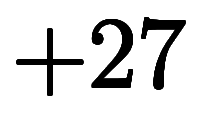 ¤ňÉáÄ̤ˤą¤Č*3ˇ˘Ěµ¸Â¤Î·«¤ęľĺ¤¬¤ę¤Çľĺ°Ě¤¬
¤ňÉáÄ̤ˤą¤Č*3ˇ˘Ěµ¸Â¤Î·«¤ęľĺ¤¬¤ę¤Çľĺ°Ě¤¬ ¤Ë¤Ę¤ë¤Î¤¬łÎǧ˛ÄÇ˝ˇŁ
¤Ë¤Ę¤ë¤Î¤¬łÎǧ˛ÄÇ˝ˇŁ
| Ą¤ł¤¦¤·¤Ćˇ˘˛Ľ°Ě¤«¤é1¤ňĚ㤤ˇ˘ľĺ°Ě¤Ë1¤ň˛ˇ¤·˝Đ¤ą·ë˛Ěˇ˘0¤¬ÎĚ»ş¤µ¤ě¤ë |
| ˇ ŽĄŽĄ973¤Îľĺ°Ě¤Ë9¤¬Ěµ¸Â¤ËÂł¤¤¤Ć¤¤¤ë |
| ˘ °ě¤Î°Ě¤Î3ˇÜ7¤Ç·«¤ęľĺ¤¬¤ę¤¬ČŻŔ¸¤·ˇ˘˝˝¤Î°Ě¤¬8¤Ë¤Ę¤ë |
|
¶ńÂÎÎă¤Č¤·¤Ćˇ˘´ű¤Ë˝Đ¤Ć¤¤ż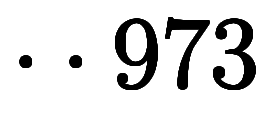 ¤Ë
¤Ë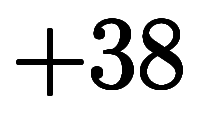 ¤ňÉáÄ̤ˤą¤Č°Ę˛Ľ¤Ë¤Ę¤ëˇ§
¤ňÉáÄ̤ˤą¤Č°Ę˛Ľ¤Ë¤Ę¤ëˇ§
|
|
|
|
ŔäÂĐĂÍÉ˝¸˝¤ËÂФ·ˇ˘Ééąć¤Ë±ţ¤¸¤Ć±é»»Ą˘ĄëĄ´ĄęĄşĄŕ¤ňĘѤ¨¤ëɬÍפ¬Ěµ¤¤¤Î¤¬ĘäżôÉ˝¸˝¤Î¶Ż¤ßˇŁ
ĽÂşÝˇ˘Ŕ¤¤ÎĂć¤Î·×»»µˇ¤Ď2¤ÎĘäżôÉ˝¸˝¤ň»Č¤Ă¤Ćˇ˘żô¤ÎÉäąć¤Çľěąçʬ¤±¤»¤ş¤ËŔ°żô¤ň˛Ă¸ş¤·¤Ć¤¤¤ëˇŁ
¤ł¤Î¤č¤¦¤Ëˇ˘É˝µ¤ňą©Éפą¤ë¤ł¤Č¤Çˇ˘Ą˘ĄëĄ´ĄęĄşĄŕ¤¬´Ęñ¤Ë¤Ę¤ë¤ł¤Č¤¬Âżˇą¤˘¤ë*4ˇŁ



É®»»¤Î˝ń¤Ęý¤ĎŔΤ䳰ąń¤Ţ¤ÇĚܤň¸ţ¤±¤Đż§¤ó¤Ę˝ń¤Ęý¤¬¤˘¤ëˇŁ
¶µ˛Ę˝ń¤ËşÜ¤Ă¤Ć¤¤¤ë¤Î¤Ď°ěÎă¤Ç¤·¤«¤Ę¤¤ˇŁ