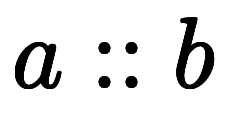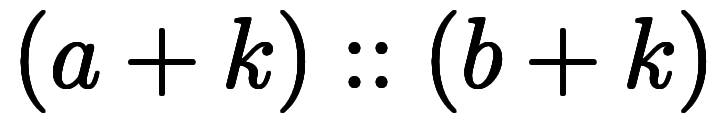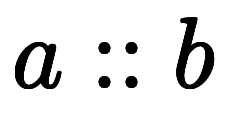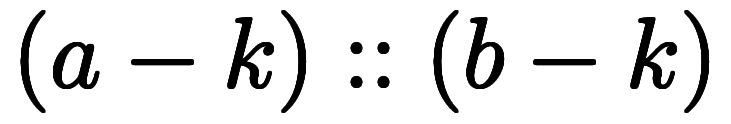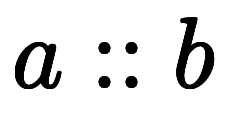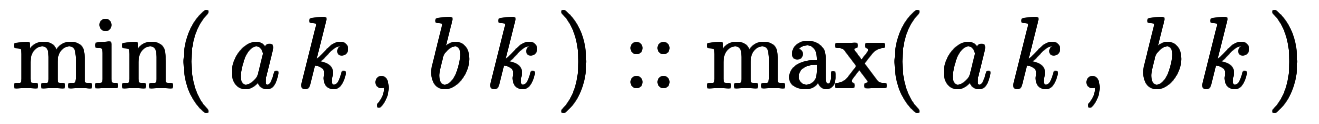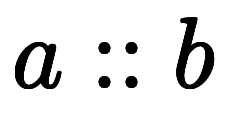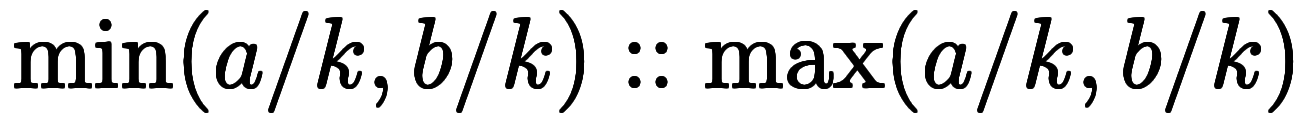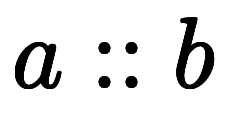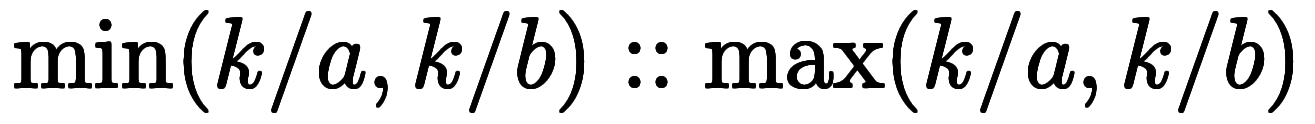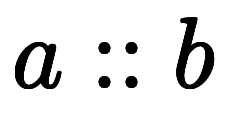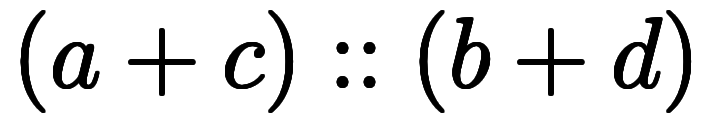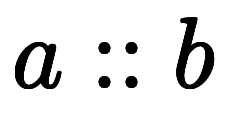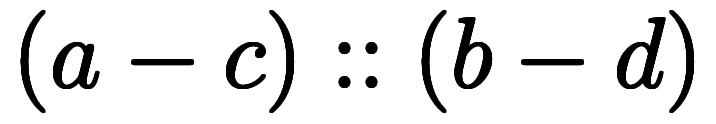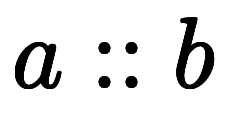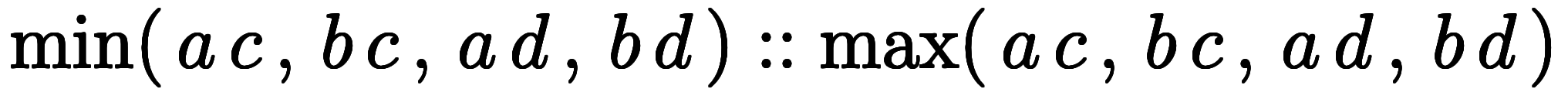区間表記 EditToHeaderToFooter

数学では定義域、積分区間など、整数や実数における区間が登場する。
主に以下の表記が用いられているが、それぞれ短所があり、区間演算の記述が煩雑になる。

表記文脈短所
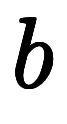$$ a $$≦$$ x $$＜$$ b $$簡易的な表記変数が明示的に定義されてない場合に利用不可
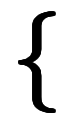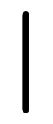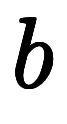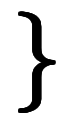$$ \{ $$$$ x $$$$ \pipe $$$$ a $$≦$$ x $$＜$$ b $$$$ \} $$集合としての表記表記が煩雑*1
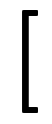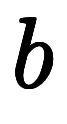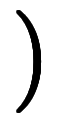$$ [ $$$$ a $$$$ , $$$$ b $$$$ ) $$大学や論文などで用いられる表記括弧の他の用法と紛らわしく、半開区間では丸括弧と角括弧が混在して可読性が悪い。
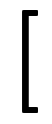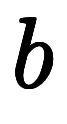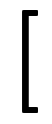$$ [ $$$$ a $$$$ , $$$$ b $$$$ [ $$括弧の他の用法と紛らわしい、半開区間では同じ向きの括弧が対を成し可読性が悪い。
$$ \int_a^b $$〜$$ ,\; $$$$ \bigg[ $$〜$$ \bigg]_a^b $$定積分積分における特殊表記。汎用性に欠ける。

これらに対し、凌宮数学では汎用性と利便性を考慮し、下記区間表記を用いる：

  • $$ a {.}{.} b $$$$ = $$$$ \{ $$$$ x $$$$ \pipe $$$$ a $$＜$$ x $$＜$$ b $$$$ \} $$
  • $$ a {.}{:} b $$$$ = $$$$ \{ $$$$ x $$$$ \pipe $$$$ a $$＜$$ x $$≦$$ b $$$$ \} $$
  • $$ a {:}{.} b $$$$ = $$$$ \{ $$$$ x $$$$ \pipe $$$$ a $$≦$$ x $$＜$$ b $$$$ \} $$
  • $$ a {:}{:} b $$$$ = $$$$ \{ $$$$ x $$$$ \pipe $$$$ a $$≦$$ x $$≦$$ b $$$$ \} $$

区間演算 EditToHeaderToFooter

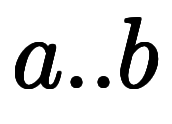
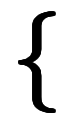
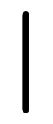
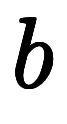
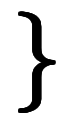
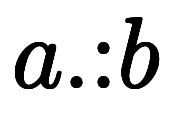
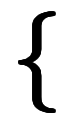
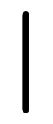
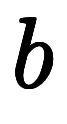
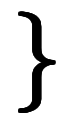
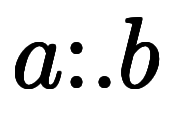
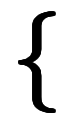
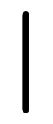
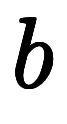
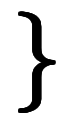
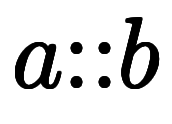
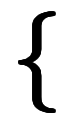
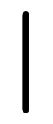
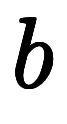
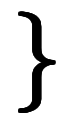
一般に、区間演算は次のように定義される：

  • $$ a::b $$$$ + $$$$ k $$$$ = $$$$ (a+k)::(b+k) $$
  • $$ a::b $$$$ - $$$$ k $$$$ = $$$$ (a-k)::(b-k) $$
  • $$ a::b $$$$ \;\sx\, $$$$ k $$$$ = $$$$ \min(\,a\,k\,,\,b\,k\,)::\max(\,a\,k\,,\,b\,k\,) $$
  • $$ a::b $$$$ \, / \, $$$$ k $$$$ = $$$$ \min(a/ k,b/ k)::\max(a/ k,b/ k) $$
  • $$ k $$$$ \, / \, $$$$ a::b $$$$ = $$$$ \min(k/ a,k/ b)::\max(k/ a,k/ b) $$
  • $$ a::b $$$$ + $$$$ c::d $$$$ = $$$$ (a+c)::(b+d) $$
  • $$ a::b $$$$ - $$$$ c::d $$$$ = $$$$ (a-c)::(b-d) $$
  • $$ a::b $$$$ \;\sx\, $$$$ c::d $$$$ = $$$$ \min(\,a\,c\,,\,b\,c\,,\,a\,d\,,\,b\,d\,)::\max(\,a\,c\,,\,b\,c\,,\,a\,d\,,\,b\,d\,) $$
  • $$ a::b $$$$ \, / \, $$$$ c::d $$$$ = $$$$ a::b $$$$ \;\sx\, $$$$ \ffd1c{::}\ffd1d $$

まとめ・つなぎ EditToHeaderToFooter

参考文献 EditToHeaderToFooter
*1 この場合の$$ x $$は内部変数であるため、$$ x $$単独で短所ではないものの、大量に使う場合$$ x $$に統一すると紛らわしく、異なる名前にすると用意するのが煩わしい問題を抱えている。
リロード   新規 編集 凍結 差分 添付 複製 改名   数学 一覧 検索 最新 バックアップ リンク元   ヘルプ   最終更新のRSS
Last-modified: 2015.1002 (金) 2136.3700 (3128d)