![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
積分定数 |
凌宮表記術: |
|||||||||||||||||||||||||||||
|
凌宮数式の定数表記を使うと、とりあえず次のように書ける。
|
ここで、積分と微分の関係から、 は
は

 を意味すると理解しても良い。
を意味すると理解しても良い。



問題は多変数関数の場合。
|
理系の大学生はこれを見せられる上、「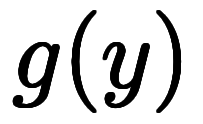 は任意関数」や「
は任意関数」や「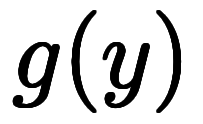 は
は だけの関数」のような但し書きを教わる。
だけの関数」のような但し書きを教わる。
そして「1変数のときと同じよね」と言われる。
この謎の関数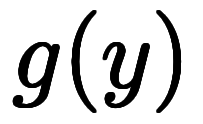 が積分定数
が積分定数 に対応するのは位置で勘ぐれなくもないが、
に対応するのは位置で勘ぐれなくもないが、
これで何がどう同じなのかまで分かれというのは無茶な話。
1変数関数と多変数関数で、一体何が同じで、何が異なるのかは、こんな表で考えれば良い:
表1: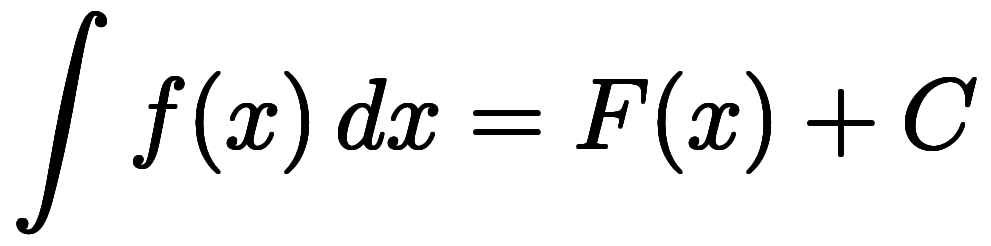 の の と変数の関係 と変数の関係 | ||
|---|---|---|
 は は の定数 の定数 |  は は の関数 の関数 | |
| ◎ | × | |
表2: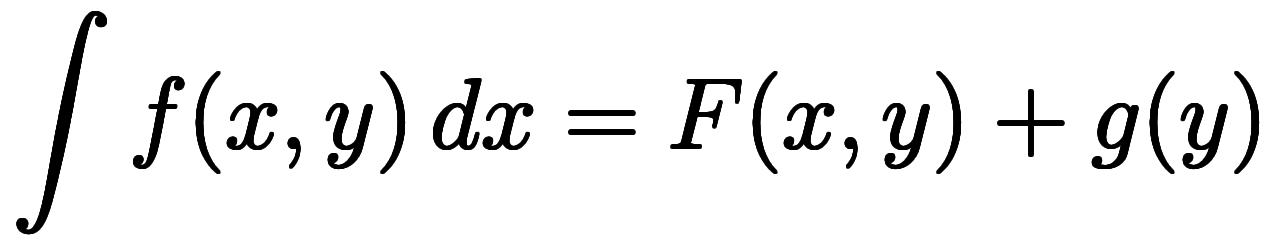 の の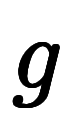 と変数の関係 と変数の関係 | ||
|---|---|---|
 は は の定数 の定数 |  は は の関数 の関数 | |
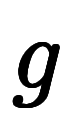 は は の定数 の定数 | ◎ | × |
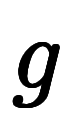 は は の関数 の関数 | ◎ | × |
つまり、 で積分するときに重要なのは、
で積分するときに重要なのは、 の定数であることであって、
の定数であることであって、 の関数かどうかではない*1
の関数かどうかではない*1
この事実を素直に定数表記で表現すると次のようになる:
1変数: |
2変数: |
被積分関数 が1変数の
が1変数の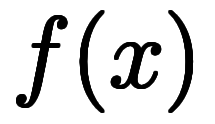 から2変数の
から2変数の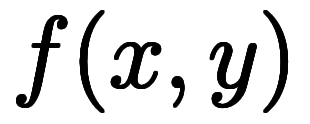 に変わっていることを除けば、少なくとも見た目は同じである。
に変わっていることを除けば、少なくとも見た目は同じである。
さらに同じ部分を抜き出すと、より洗練された記述が得られる:
|
これこそ何変数でも成り立つ不定積分のあるべき姿。