![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
反変ベクトルと共変ベクトル |
反変ベクトルと共変ベクトル |
|



一般に、任意のベクトル に対し、その
に対し、その 成分はベクトルと逆基底ベクトルの内積で与えられる。
成分はベクトルと逆基底ベクトルの内積で与えられる。
|
|
正基底 が
が 倍に変わる場合、
倍に変わる場合、
正基底の成分は逆基底の付き方から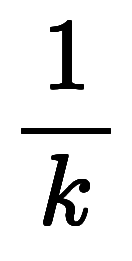 倍に変わることが直ちに分かる。
倍に変わることが直ちに分かる。
|
他方、逆基底の成分は正基底で割算するため、

 倍に変わるのは容易に予想できる。
倍に変わるのは容易に予想できる。
|



一般に、任意のベクトル と
と は一対の反変と共変表記により成分同士の積和形で表せる。
は一対の反変と共変表記により成分同士の積和形で表せる。
| |
|
|
|
正基底を 倍したところで、逆基底が
倍したところで、逆基底が 倍になり、全体では変わらないのが分かる。
倍になり、全体では変わらないのが分かる。
歴史的に、ベクトルを成分のみで表す習慣が根強い。
そのため、反変成分で表記されるベクトルを反変ベクトル、
他方では、共変成分で表記されるベクトルを共変ベクトルと呼ばれる。
同一のベクトルでも表記次第で反変ベクトルにも共変ベクトルにもなるため、
反変ベクトルと共変ベクトルの区別はベクトル自体の性質ではない。
しかし、名前からベクトルの種類と勘違いされ易く、学者*2には注意が必要である*3。
特に内積においては、反変成分と共変成分の組合せで基底を書かずに済むため、
片方のベクトルを反変成分で、他方を共変成分で表す表記法が多用される。
その結果、物理学ではベクトル量毎に表記法が決められる場合もある*4。



習慣的に、ベクトル幾何では長さの基底を正基底とする。
位置ベクトルや微小変位ベクトルでは共変基底が多用される。
例:
|
|
関連して、任意のスカラー場*5 の全微分に関し、
の全微分に関し、
 の勾配ベクトル
の勾配ベクトル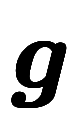

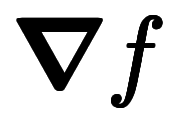 と微小変位
と微小変位 が内積関係にある:
が内積関係にある:



 。
。
そのため、 を共変基底と反変成分で表す場合、勾配は反変基底と共変成分で表される。
を共変基底と反変成分で表す場合、勾配は反変基底と共変成分で表される。
その習慣のため、勾配が共変ベクトルの代表例に選ばれ易い。
|
|
|
逆基底表記を使うと次のように書ける:
|
|
簡単な例として、1次元における関数


 の勾配を考えると、
の勾配を考えると、


 が勾配の共変成分に該当するのが分かる。
が勾配の共変成分に該当するのが分かる。
|
正基底を 倍にして、
倍にして、


 なる座標系を考えると、
なる座標系を考えると、
ベクトルの座標不変性で



 が成立し、
が成立し、 は
は





 になる。
になる。
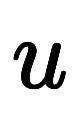


 を
を に代入すると、
に代入すると、


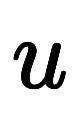 が得られて、
が得られて、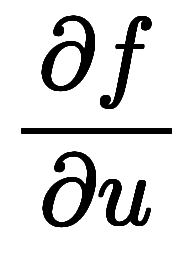 が求まる。
が求まる。
|
|
|
|


