![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
もし微分が陰関数を基準で表記されたら【編集中】【ネタ】 |
概要 |
|
すると、上記の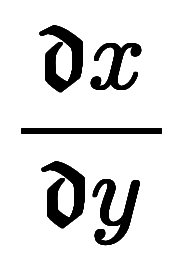

![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png)
 を偏微分の定義式に代入すると、負の偏微分の定義式が得られる:
を偏微分の定義式に代入すると、負の偏微分の定義式が得られる:
|
もしくは、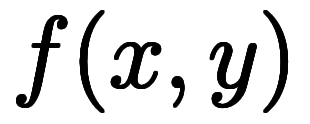 基準に拘るなら、細かいことを気にせず次のように改めれば良い:
基準に拘るなら、細かいことを気にせず次のように改めれば良い:
|



負の微分係数は、正の偏微分に負号を付けただけなため、微分の性質は全て保存される。
ただし、

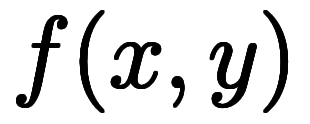 、
、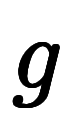

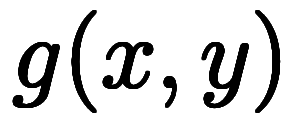 、
、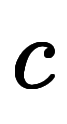

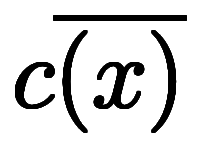 *2について考える。
*2について考える。
定数倍 |
| 乗算 |
|
|
| ||
加減算 |
| 除算 |
|
|
|



1変数の陽関数(=2変数の陰関数)の場合、

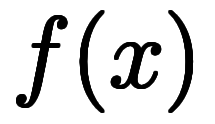 について、
について、
微分 に対応する負の微分は
に対応する負の微分は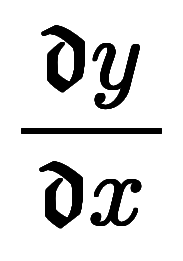

![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png)
 になる。
になる。
すると、aからbまでの不定積分は以下のようになる。
|
|
|





