![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
ベクトル微分演算子 |
凌宮表記術: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
関数表記: |
ナブラ表記では、ベクトル演算子を利用しているため、計算にベクトル演算の公式が利用できるなど、関数表記より表現力が高い。
ところが、ナブラを微分対象の左隣に書くという制約のため一部のベクトル計算で支障が出る*1*2。
また、分数形でないため、高校で習うスカラ微分の連鎖則や小学校で習う約分の感覚が途絶えてしまう。
これに対し、凌宮数学では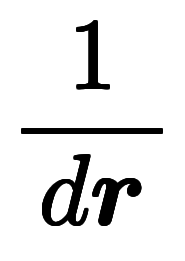 でベクトルを、
でベクトルを、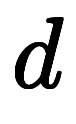 で微分対象を示し、ベクトル微分演算子を以下のように定義する。
で微分対象を示し、ベクトル微分演算子を以下のように定義する。
これより、ベクトル演算と微分演算を表記上で分離する。
| 勾配 | 回転 | 発散 | ||
|---|---|---|---|---|
| 関数表記 | 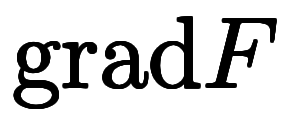 | 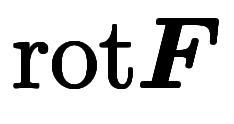 | 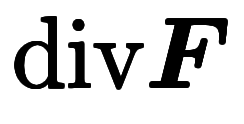 | |
| ナブラ表記 | 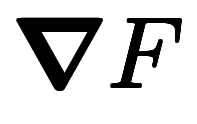 | 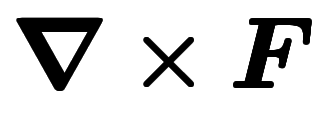 | 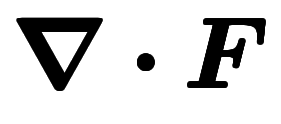 | |
| 凌宮表記 | 分数形 |  | 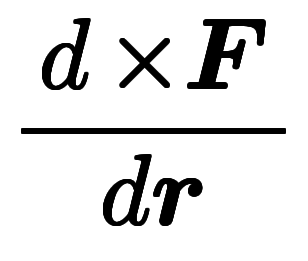 |  |
| 関数形 |  | 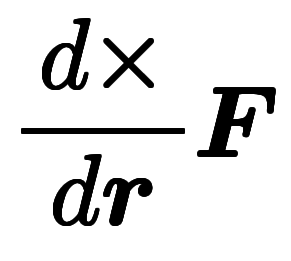 | 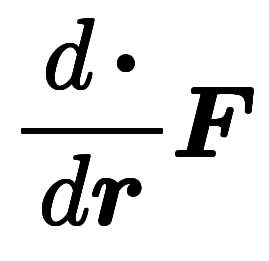 | |
| 演算子形 | 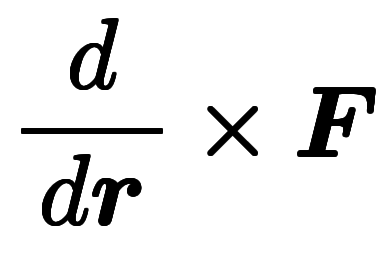 |  | ||
| 分離形 | 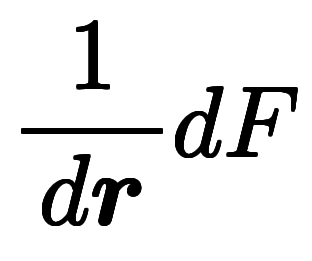 | 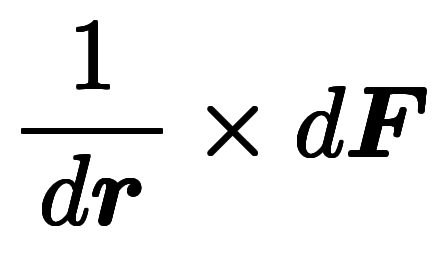 | 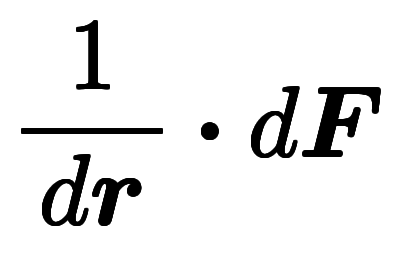 | |
まず見た目は、上から下に向かって表記が分離されていく形となる。
分数形は連鎖側のための書式である。
関数形は関数表機、演算子形はナブラ表記に互換性を持つ書式である。
分離形は微分演算とベクトル演算を別々計算するための書式である。
これらの間は分数の感覚で自由に行き来できるように工夫している。
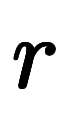 がスカラの場合、
がスカラの場合、 が
が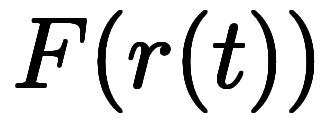 に対する連鎖則。
に対する連鎖則。
分数形で記述する場合、あくまでも形式的だが、約分の感覚で直観的に式変形できる。
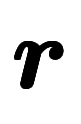 がベクトルの場合、
がベクトルの場合、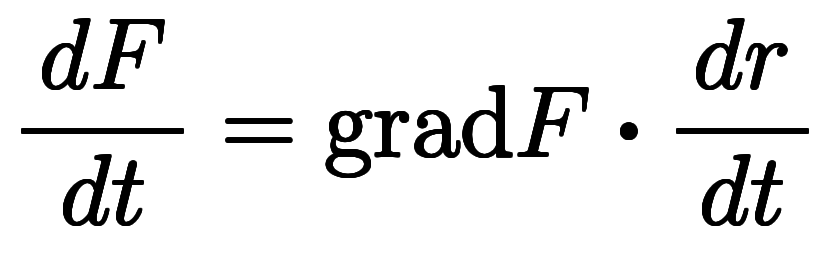 が
が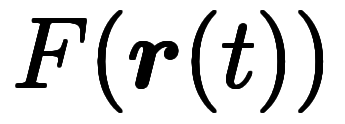 に対する連鎖則。
に対する連鎖則。
ナブラ表記でも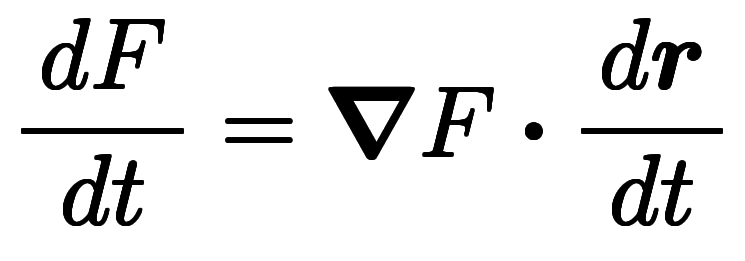 と、表現力においては関数表記と大差ない。
と、表現力においては関数表記と大差ない。
これらに対し連鎖則を凌宮表記の分数形で書けば、 になる。
になる。
スカラの積がスカラ積になることを除けば、分数の姿がそのまま生き残り、式を直感的に操作できる。
もっとも、スカラが1次元のベクトルで、その場合のスカラ積がスカラの積になるため、ベクトルの式がスカラの式を名実とも含むことになる。
ベクトルの外積は のように、交換則の代わりに、交代則が成り立つ。
のように、交換則の代わりに、交代則が成り立つ。
一方、ナブラは右側しか微分しないため、 と書けない。
と書けない。
高が符号一つだが、回転に対応する外積の交代則を記述できないがために、回転を含む微分演算の妨げになる。
凌宮表記の分離形を使えば、交代則は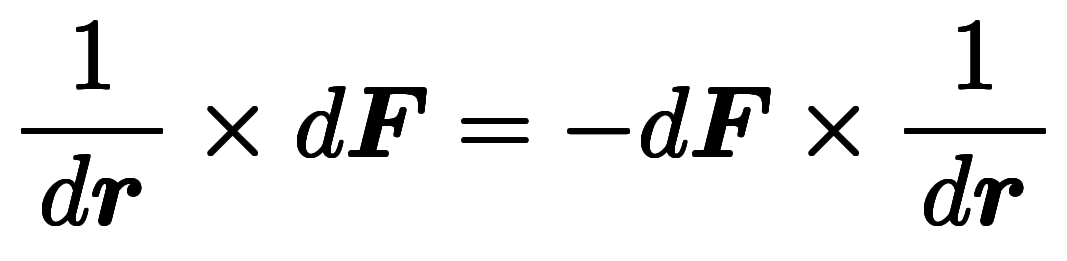 と書ける。
と書ける。
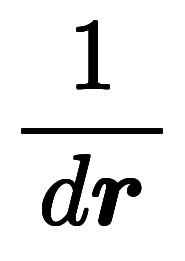 は最初に出会う
は最初に出会う が指し示す相手を微分するため、順番は関係ない。
が指し示す相手を微分するため、順番は関係ない。
これより、ベクトル外積の公式を適応するときに微分演算子を考慮する必要がなくなる。
外積の勾配の公式:
|
|
関数表記でもナブラ表記でも表記が互いに制約して式変形ができない。
このため、似たような公式を丸覚えする羽目になる。
これを凌宮表記の分離形を使えば、積の微分、スカラ三重積の交換則、外積の交代則から形式的に導けるようになる。
ここで使う法則は以下の3つである:
積の微分: | |
スカラ三重積の交換則: |
|
外積の交代則: |
|
凌宮表記の分離形で外積の勾配を導くと次のように記述できる。
遊離した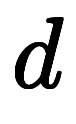 は自由に動けるため、微分対象を
は自由に動けるため、微分対象を の左に置いても問題ないのが鍵である。
の左に置いても問題ないのが鍵である。
| |
| 積の微分 |
| スカラ三重積の交換則 |
| 外積の交代則 |
さすがに従来表記では教育の立場では不便過ぎて、先生たちもそれぞれが記号を工夫して教えている。
良く見かける手法として、ナブラと作用対象を線または矢印で結ぶ記法がある。
この作用対象を表す線は、凌宮表記の作用対象を表す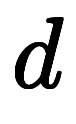 と微分ベクトルにある
と微分ベクトルにある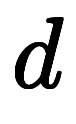 のペアリングを表現しているに等しい。
のペアリングを表現しているに等しい。
| |
| 積の微分 |
| スカラ三重積の交換則 |
| 外積の交代則 |
ベクトル微分は、微分ベクトル、微分対象とこれらの微分演算で構成される。
このため、凌宮数学のように機能毎に表記を割り当てれば、微分やベクトルの基本的な公式を利用した式変形が可能になる。
分離型の利点として、回転とスカラ三重積の公式しか紹介してないが、
他にも回転とベクトル三重積を含む公式と応用範囲が広い:ベクトル微分演算子/回転公式
また、3次元の正規直交座標系では、 の正体は
の正体は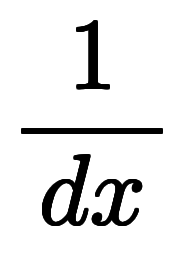 、
、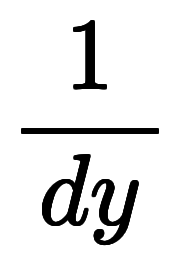 、
、 を成分とするベクトルである。
を成分とするベクトルである。
これは表記の通り、凌宮数学の逆基底と深く繋がっている。
その話は微分の根底に繋がるため、いずれの機会で纏める予定。