加法定理
加法定理は、加減算の三角関数を分解する公式。便宜上、三角関数が か
か のどちらかで未定であることを
のどちらかで未定であることを と表記すると*1、加法定理は次のように書ける:
と表記すると*1、加法定理は次のように書ける:
重要なのは と
と は加算を乗算に変える能力を持っていること*2。そして、これが次の指数の法則と同じ形であること。
は加算を乗算に変える能力を持っていること*2。そして、これが次の指数の法則と同じ形であること。
等号ではないのは、符号や係数などが欠けているため。式の左辺がそれぞれ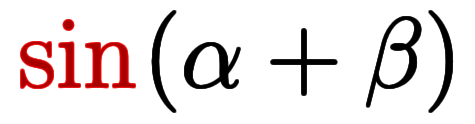 、
、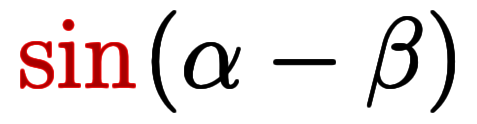 、
、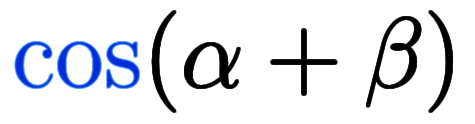 、
、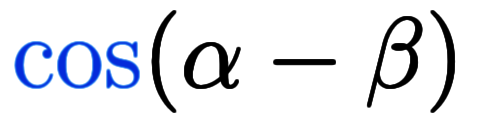 の場合について、等号が成立するように右辺を決めて行くのが組立の仕事。
の場合について、等号が成立するように右辺を決めて行くのが組立の仕事。
語源は三角を意味する英語 triangle の先頭で「三」を意味する三文字の語根 tri から。
公式なんかより関数の性質を覚える方が遥かに重要
1. 正弦合わせ
組立は の決定から始める。三角関数は三角公式の骨組みのようなもので、これが決まらないと何も決まらない。
の決定から始める。三角関数は三角公式の骨組みのようなもので、これが決まらないと何も決まらない。
猫式では、個々の項に対し、乗算している の数をその項の正弦数と定義する。加法定理の右辺にある
の数をその項の正弦数と定義する。加法定理の右辺にある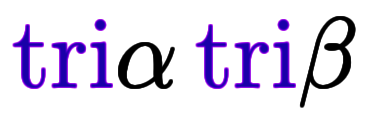 には未定表記が2つあるため、組み合せは2×2=4通り。それぞれの正弦数は次のようになる:
には未定表記が2つあるため、組み合せは2×2=4通り。それぞれの正弦数は次のようになる:
そして、正弦数に関して組立術の真髄である次の規則が成り立つ:
正弦陰性則:  が2つ掛け合わせる毎に、項の前に「 が2つ掛け合わせる毎に、項の前に「![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」が1つ増える 」が1つ増える |
正弦奇偶則: 正弦数は、等式の各項を通して「全て奇数」または「全て偶数」 |
これらを適応すると、右辺はそれぞれ2組ずつ絞られる:
等式にするため、2つの候補から1つの値を作ることになるが、ここは加法定理ということで単純に加えば良い*3。ここまでの作業で次の形になる:
和積公式でも同じ状況になるが、和積は右辺が積なので、加えない。
2. 符号合わせ
続けて、式に残る符号を決める。一般に、数式は上手くできるもので、「 」が基本で、何かの理由があって初めて「
」が基本で、何かの理由があって初めて「![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」が現れる。というわけで、左辺が加算の2式は「
」が現れる。というわけで、左辺が加算の2式は「 」が「
」が「![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」に化ける理由が無いから、もう出来上がっている。
」に化ける理由が無いから、もう出来上がっている。
残りの2式は、左辺の が符号反転したがために、右辺でも符号反転する。しかし、次のように書いた場合、反転する符号は選ぶ余地が無いよう見えるが、
が符号反転したがために、右辺でも符号反転する。しかし、次のように書いた場合、反転する符号は選ぶ余地が無いよう見えるが、
2つの候補を逆に書いた場合、通常省略される![\clr[ao]+ $$ \clr[ao]+ $$](./eq/eq-ni-af851260f168d784a9e2d74aa715377a.png) が現われ、反転することになる
が現われ、反転することになる![\clr[mr]+ $$ \clr[mr]+ $$](./eq/eq-ni-33612a2ad36c111b6408acaa434fe8bc.png) が省略されるので困る。
が省略されるので困る。
このため、目に見える符号の反転ではなく、「項の符号反転」として全ての項について考える必要がある。
結果的に、右辺の を
を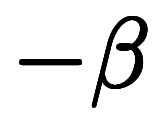 に置き換えて計算することになるが、
に置き換えて計算することになるが、 は
は![\ccos(\iro[ak]- \beta) $$ \ccos(\iro[ak]- \beta) $$](./eq/eq-ni-d8200d22b2aab1d8576496dbf90a19c5.png)
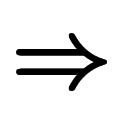
 と「
と「![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」を消すのに対し、
」を消すのに対し、 は
は![\csin(\iro[ak]- \beta) $$ \csin(\iro[ak]- \beta) $$](./eq/eq-ni-2efd7e71c2370e5fa199c62f3c6696f8.png)

![\iro[ak]- \csin(\beta) $$ \iro[ak]- \csin(\beta) $$](./eq/eq-ni-60d671d6801efbc140be717b17fefd5b.png) と「
と「![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」を通す性質*4を使えば良い。
」を通す性質*4を使えば良い。
また、色で直感的に覚えても良い。正弦陰性則でも、「![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」を伝搬する性質でも、
」を伝搬する性質でも、 は「
は「![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」と相性が良い。
」と相性が良い。 と「
と「![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」を赤で統一しているのもこのためである。
」を赤で統一しているのもこのためである。
以上の結果、加法定理の4式は次のようになる。
専門用語では、 は偶関数、
は偶関数、 は奇関数。
は奇関数。 3. 値域合わせ
本来なら、最後は値域をチェックする段取りだが、この場合、右辺の値域は簡単には分らない*5。幸いなことに、数式は上手くできるもので、簡単に分らないからチェックしなくても良い。既に上手くできているから。
「簡単」というのは、加算(or減算)と乗算を1回ずつで出せることを意味し、専門用語では線形変換という。非線形になる途端に解けなくなる場合は結構あるので、こういうセンスも重要である。
リンク
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)