和積公式
和積公式は、三角関数の和を三角関数の積に変換する公式。未定記号を使うと、
今度は、 と
と がそれぞれ
がそれぞれ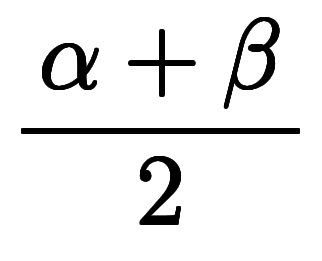 と
と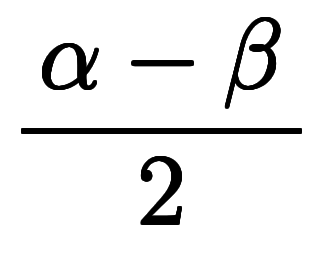 で、
で、
積和と和積で引数が紛らわしいが、積和は右辺が和なので和の形をした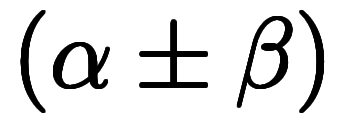 を取る、和積は右辺が積のため積の形をした
を取る、和積は右辺が積のため積の形をした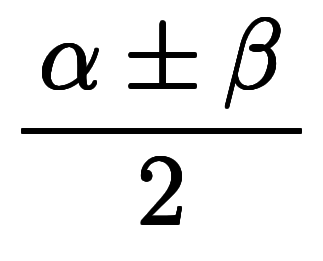 を取るとでも覚えば良い。
を取るとでも覚えば良い。
1. 正弦合わせ
式の左辺には未定記号が3つあるため、組合せは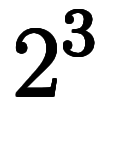

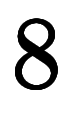 通り。しかし、これまでと異なり、正弦奇遇則に違反するために不可となる組み合わせが現れる。正弦奇偶則と正弦陰性則を適応すると、次のようになる:
通り。しかし、これまでと異なり、正弦奇遇則に違反するために不可となる組み合わせが現れる。正弦奇偶則と正弦陰性則を適応すると、次のようになる:
ここも加法定理と紛らわしく右辺の候補に対して2択1を取るのだが、和積は右辺が積のため既に積の形をした候補から2択1すれば良い。
2. 符号合わせ
続けて、左辺の符号に応じて、右辺を決める。今度は と
と を交換して、式の値を調べる。左辺は「
を交換して、式の値を調べる。左辺は「 」なら変化無し、「
」なら変化無し、「 」なら変化有り。右辺は
」なら変化有り。右辺は が符号反転するため、
が符号反転するため、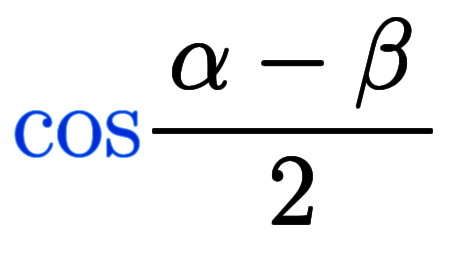 を持つ方が変化無し、持たない方が変化有り。
を持つ方が変化無し、持たない方が変化有り。
3. 値域合わせ
今、左辺は三角関数の和のため値域は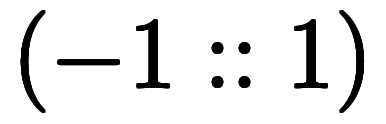

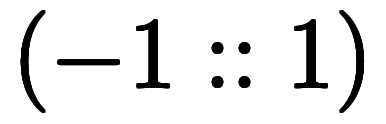

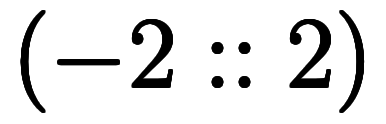 、右辺は三角関数の積のため値域は
、右辺は三角関数の積のため値域は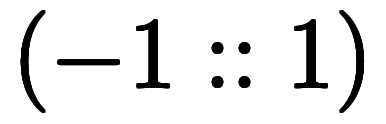

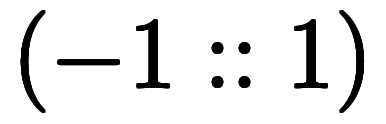

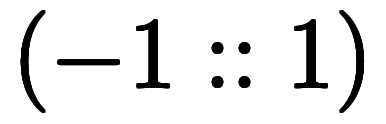 。このため、値域を合わせるには、右辺を
。このため、値域を合わせるには、右辺を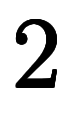 倍すれば良い。
倍すれば良い。
以上より、和積公式の4式は次のようになる。
リンク
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)